In Figure, lines AB and CD intersect at O. If ∠AOC+ ∠BOE=700and ∠BOD=400, find ∠BOE and reflex ∠COE
To solve the problem step by step, we will follow the reasoning outlined in the video transcript.
Step 1: Identify the Given Information
We have two lines AB and CD intersecting at point O. The following angles are given:
- ∠AOC+∠BOE=70∘
- ∠BOD=40∘
Step 2: Use the Property of Vertically Opposite Angles
Since lines AB and CD intersect at O, we know that vertically opposite angles are equal. Therefore:
∠BOD=∠AOC
Given that ∠BOD=40∘, we can conclude:
∠AOC=40∘
Step 3: Substitute to Find ∠BOE
From the equation ∠AOC+∠BOE=70∘, we can substitute the value of ∠AOC:
40∘+∠BOE=70∘
To find ∠BOE, we subtract 40∘ from both sides:
∠BOE=70∘−40∘=30∘
Step 4: Use the Straight Line Property
Since AOB is a straight line, the angles ∠AOC, ∠COE, and ∠BOE must add up to 180∘:
∠AOC+∠COE+∠BOE=180∘
Substituting the known values:
40∘+∠COE+30∘=180∘
This simplifies to:
70∘+∠COE=180∘
Now, we can solve for ∠COE:
∠COE=180∘−70∘=110∘
Step 5: Find the Reflex Angle ∠COE
The reflex angle is calculated as:
Reflex ∠COE=360∘−∠COE
Substituting the value of ∠COE:
Reflex ∠COE=360∘−110∘=250∘
Final Answer
Thus, we have:
- ∠BOE=30∘
- Reflex ∠COE=250∘
---
We have two lines AB and CD intersecting at point O. The following angles are given:
- ∠AOC+∠BOE=70∘
- ∠BOD=40∘
Since lines AB and CD intersect at O, we know that vertically opposite angles are equal. Therefore:
∠BOD=∠AOC
Given that ∠BOD=40∘, we can conclude:
∠AOC=40∘
From the equation ∠AOC+∠BOE=70∘, we can substitute the value of ∠AOC:
40∘+∠BOE=70∘
To find ∠BOE, we subtract 40∘ from both sides:
∠BOE=70∘−40∘=30∘
Since AOB is a straight line, the angles ∠AOC, ∠COE, and ∠BOE must add up to 180∘:
∠AOC+∠COE+∠BOE=180∘
Substituting the known values:
40∘+∠COE+30∘=180∘
This simplifies to:
70∘+∠COE=180∘
Now, we can solve for ∠COE:
∠COE=180∘−70∘=110∘
The reflex angle is calculated as:
Reflex ∠COE=360∘−∠COE
Substituting the value of ∠COE:
Reflex ∠COE=360∘−110∘=250∘
Thus, we have:
- ∠BOE=30∘
- Reflex ∠COE=250∘
Topper's Solved these Questions
Similar Questions
In Fig. 6.13, lines AB and CD intersect at O. If ∠AOC +∠BOE=70∘and ∠BOD=40∘, find ∠BOE and reflex ∠COE.
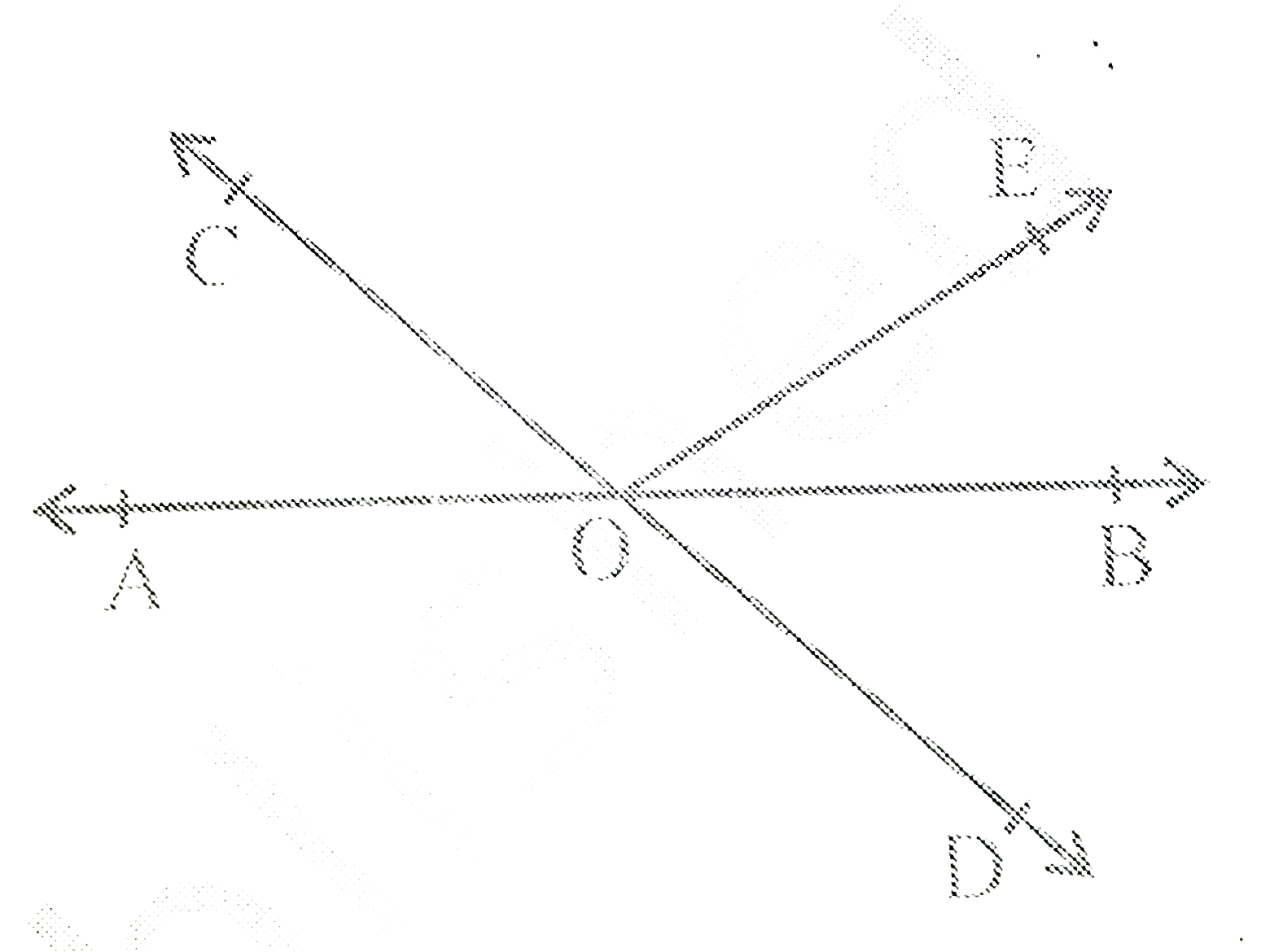
View SolutionIn Figure, lines AB, CD and EF intersect at O. Find the measures of ∠AOC, ∠COF, ∠DOE and ∠BOF .
View SolutionTwo lines AB and CD intersect at O. If ∠AOC+∠COB+∠BOD=2700 , find the measures of ∠AOC, ∠COB, ∠BOD and ∠DOA.
View SolutionTwo lines AB and CD intersect at O. If ∠AOC+∠COB+∠BOD=2700 , find the measures of ∠AOC, ∠COB, ∠BOD and ∠DOA.
View SolutionTwo straight lines AB and CD intersect one another at the point O. If ∠AOC+∠COB+∠BOD=2740, then ∠AOD=
View SolutionIn Figure, OP bisects ∠BOC and OQ bisects ∠AOC. Show that ∠POQ=900
View SolutionIn Figure, if ∠AOB=800and ∠ABC=300, then find ∠CAO
View SolutionLine segments AB and CD intersect at O such that AC∣∣DB . If ∠CAB=350 and ∠CDB=550 find the ∠BOD.
View SolutionIn Fig, OA, OB are opposite rays and ∠AOC+ ∠BOD=900, Find ∠COD.
View SolutionAB and CD are diameters of a circle with centre O. If ∠OBD=500, find ∠AOC
View Solution
