In Figure, if and find
To solve the problem step by step, we will use the properties of parallel lines and angles formed by transversals.
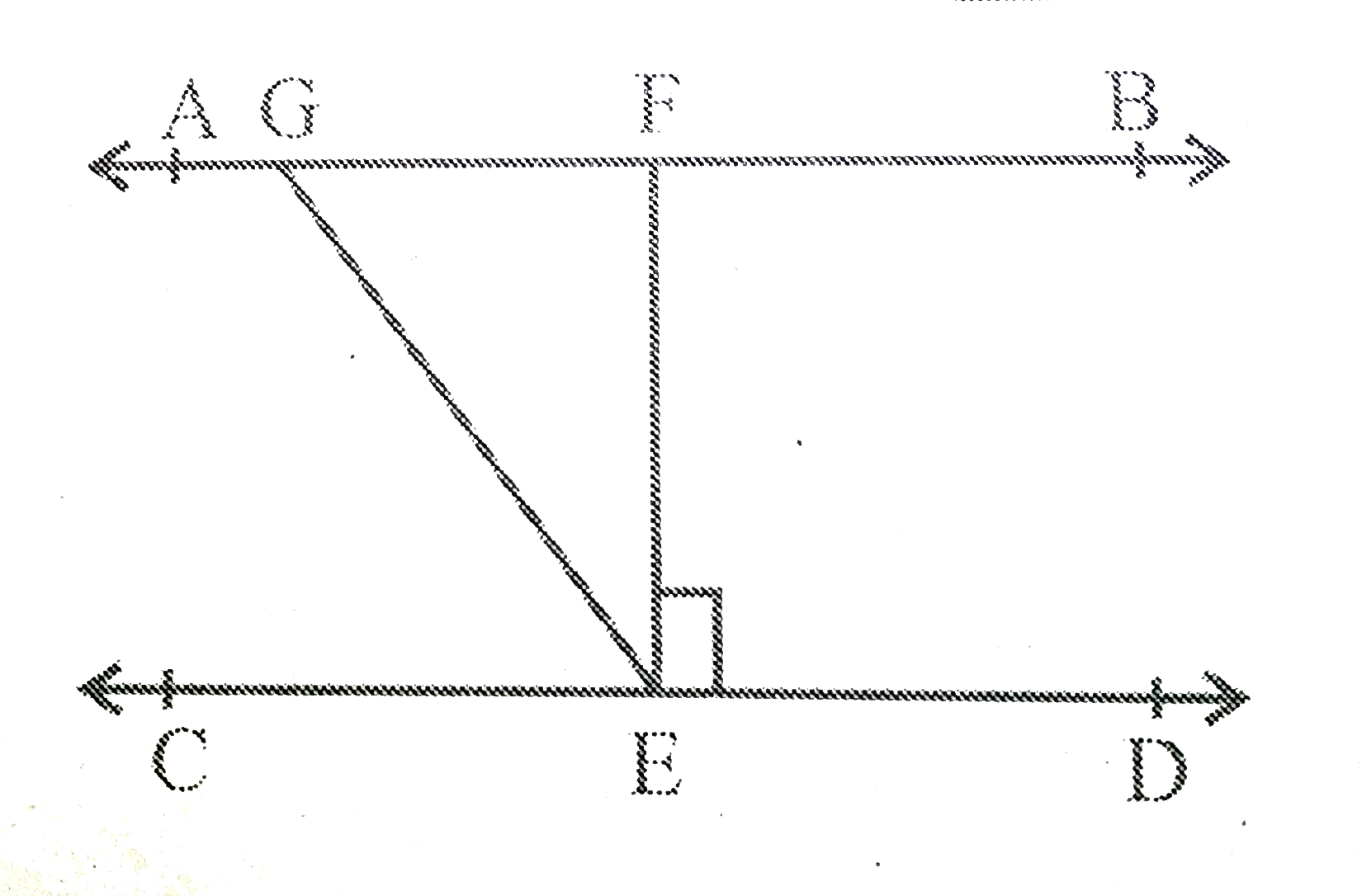
Step 1: Identify the given information
- We have two parallel lines AB∥CD.
- Line EF is perpendicular to line CD (i.e., EF⊥CD).
- The angle ∠GED=126∘.
Step 2: Find ∠AGE
Since AB∥CD and GE is a transversal, we can use the property of alternate interior angles. Therefore, we have:
∠AGE=∠GED
Substituting the value:
∠AGE=126∘
Step 3: Find ∠FGE
Since AB is a straight line, the angles ∠AGE and ∠FGE are supplementary. Thus:
∠AGE+∠FGE=180∘
Substituting the value of ∠AGE:
126∘+∠FGE=180∘
Now, solving for ∠FGE:
∠FGE=180∘−126∘=54∘
Step 4: Find ∠GEF
Since EF is perpendicular to CD, we know that:
∠FED=90∘
Now, we can find ∠GEF using the relationship:
∠GEF=∠GED−∠FED
Substituting the values:
∠GEF=126∘−90∘=36∘
Summary of Results
- ∠AGE=126∘
- ∠GEF=36∘
- ∠FGE=54∘
- We have two parallel lines AB∥CD.
- Line EF is perpendicular to line CD (i.e., EF⊥CD).
- The angle ∠GED=126∘.
Since AB∥CD and GE is a transversal, we can use the property of alternate interior angles. Therefore, we have:
∠AGE=∠GED
Substituting the value:
∠AGE=126∘
Since AB is a straight line, the angles ∠AGE and ∠FGE are supplementary. Thus:
∠AGE+∠FGE=180∘
Substituting the value of ∠AGE:
126∘+∠FGE=180∘
Now, solving for ∠FGE:
∠FGE=180∘−126∘=54∘
Since EF is perpendicular to CD, we know that:
∠FED=90∘
Now, we can find ∠GEF using the relationship:
∠GEF=∠GED−∠FED
Substituting the values:
∠GEF=126∘−90∘=36∘
- ∠AGE=126∘
- ∠GEF=36∘
- ∠FGE=54∘
Topper's Solved these Questions
Similar Questions
In Fig. 6.30, if AB∣∣CD, EF⊥CD and ∠GED=126∘, find ∠AGE,∠GEF and ∠FGE.
View SolutionIn Figure, if AB||CD, EF||BC, ∠BAC=65∘ and ∠DHF=35∘, find ∠AGH.
View SolutionIn Figure, If AB||CD, CD||EF and y:z=3:7, find x.
View SolutionIn Figure, AB∣∣CD and ∠F=30∘ . Find ∠ECD.
View SolutionIn Figure, If AB||CD and CD ||EF, Find ∠ACE.
View SolutionIn Figure, AB|| CD and EF||DQ Determine ∠PDQ, ∠AED and ∠DEF
View SolutionIn Fig. 4.89, if EDC~EBA, ∠BEC=115o and ∠EDC=70o . Find ∠DEC, ∠DCE, ∠EAB, ∠AEB and ∠EBA . (FIGURE)
View Solution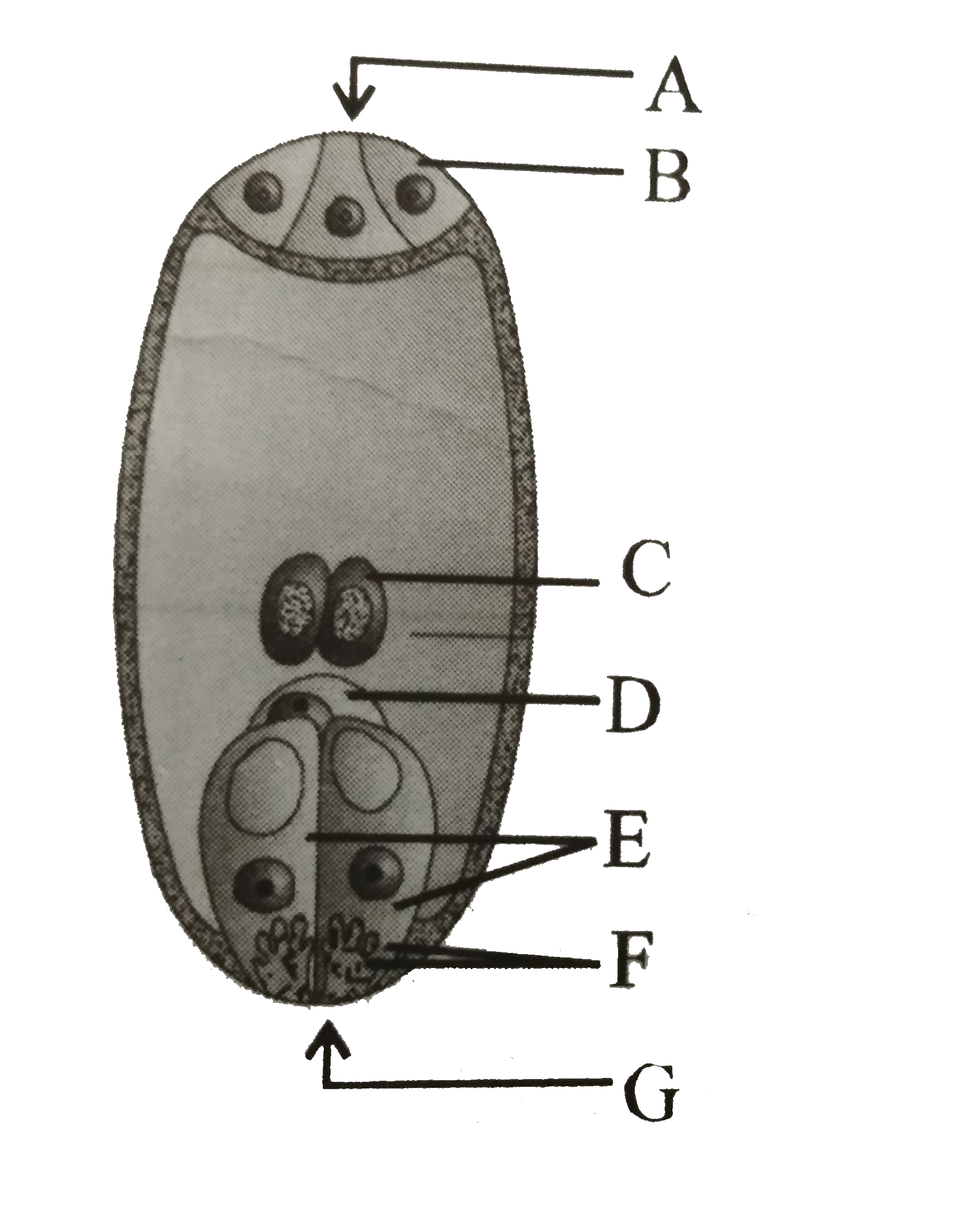
Identify A, B, C, D, E, F,G
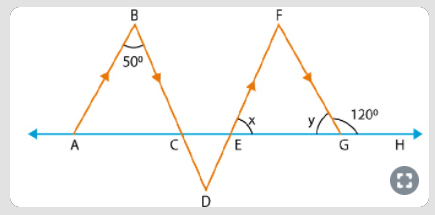
View SolutionIn Figure, if AB∣∣DF and BD∣∣FG such that ∠FGH=120∘ and ∠B=50∘, find x and y.
View SolutionIn Figure, ABCD & CDEF . Also, EA ⊥AB. If ∠BEF=550, find the values of x, y and z.
View Solution