ABCD is a parallelogram. AD is a produced to E so that DE=DC and EC produced meets AB produced in F. Prove that BF=BC.
ABCD is A parallelogram
BF=BC
In △DCE,DE=DC(given)
∠DCE=∠DEC(1)(Equal sides have equal is opposite to them)
AB∥CD,∠DCE=∠BFC(2) (pair of corresponding ∠S)
Form (1) and (2),∠DEC=∠BFC
In △AEF,∠AEF=∠AFE
AF=AE
⇒AB+BF=AD+DE
BF=AD(AB=CD=DE)
⇒BF=BC(AD=BC) Hence proved.
Topper's Solved these Questions
Similar Questions
ABCD is a parallelogram in which BC is produced to E such that CE=BC.AE intersects CD at F. Prove that ar ( ADF)= ar ( ECF) If the area of DFB=3 cm2, find the area of ^(gm) ABCD
View SolutionABCD is a parallelogram. E is a point on BA such that BE=2 EA and F is a point on DC such that DF=2 FC. Prove that AE CF is a parallelogram whose area is one third of the area of parallelogram AB CD.
View SolutionABCD is a cyclic quadrilateral. ABandDC are produced to meet in E. Prove that EBC−EDA.
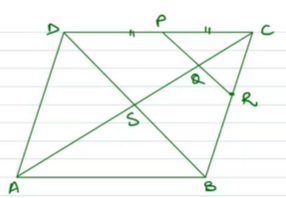
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R. Prove that R is a mid-point of BC.
 View Solution
View SolutionIn a ABC median AD is produced to X such that AD=DX . Prove that ABXC is a parallelogram.
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE and F is the point of BC such that BF=2FC. Prove that : ar(ADEG)=ar(GBCE) ar(EGB)=16ar(ABCD)
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A line through B parallel to PD meets DC at Q and AD produced at R. Prove that: AR=2BC (ii) BR=2 BQ
View SolutionABCD is a parallelogram and E is the mid-point of BC, DE and AB when produced meet at F. Then AF= 32AB (b) 2 AB (c) 3 AB (c) 54 AB
View SolutionABCD is a rhombus, EABF is a straight line such that EA=AB=BF . Prove that ED and FC when produced meet at right angles.
View SolutionABC is a triangle. D is a point on AB such that D=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC
View Solution

