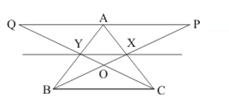
ABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP=PH
ABCD is a parallelogram, E and F are mid points of AB and DC
and a line GH intersects AD,EF and BC at G,P and H respectively.
Join GB and let it intersect EF of X.
Now since E and F are mid points of AB and DC
soAE=EB=(12)AB
and DF=FC=(12)DC
but AB=DC
so AEFD and BCFE are parallelogram
so AD||EF||BC ....... ( 1 )
Now In △ABG
AE=EBand EX∣∣AG
( From ( 1 ) )
so ,X is the mid point of GB (mid point theorem )
and in △GBH
GX=XB ( X is the mid point of GB )
so XP∣∣BH (From ( 1 ) )
so, P is the mid point of GH
so,GP=PH
Topper's Solved these Questions
Similar Questions
In a ABC,EandF are the mid-points of ACandAB respectively. The altitude AP to BC intersects FE at Q Prove that AQ=QP
View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE trisect (divide into three equal parts) the diagonal BD .
View SolutionABCD is a parallelogram and EandF are the centroids of triangles ABD and BCD respectively, then EF= (a)AE (b) BE (c) CE (d)DE
View SolutionABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM . Prove that LM and BD bisect each other.
View SolutionIn square ABCD, P and Q are mid-point of AB and CD respectively. If AB=8cm and PQ and BD intersect at O, then find area of OPB
View SolutionIn Figure, XandY are the mid-points of ACandAB respectively, QP,BCandCYQandBXP are straight lines. Prove that ar(ABP)=ar(ACQ)
 View Solution
View SolutionABC is a triangle in which D is the mid-point of BC ,E andF are mid-points of DC and AE respectively. If area of ABC is 16cm2, find the area of DEF
View SolutionABCD is a parallelogram whose AC and BD intersect at O. A line through O intersects AB at P and DC at Q. Prove that ar ( POA)= ar ( QOC).
View SolutionIn a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC=21 cm, BC=29cm and AB=30cm, find the perimeter of the quadrilateral ARPQ
View SolutionABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE=BF=CG=DH. Prove that EFGH is square.
View Solution

