ABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE=BF=CG=DH. Prove that EFGH is square.
AE=BF=CG=DH
Therefore, BE=CF=DG=AH
In △AEHand△BFE
AE=BF(Given)
∠A=∠B(each equal to 90^0)
AH=BE(By SAS criterion of congruency)
△AEH≅△BFE
.⇒EH=BF(By CPCT)
Similarity,EH=HG=GF=FE
Now,∠AEH=∠BFEand ∠AHE=∠BEF
But, ∠AEH+∠AHE=900
∠BFE+∠BFE=900
∠AEH+∠AHE+∠BFE+∠BFE=900+900
⇒∠AEH+∠BEF+∠AEH+∠BEF=1800
⇒2(∠AEH+∠BEF)=1800
⇒∠AEH+∠BEF=900
∠HEF=900
Similarly, /_EFG=/_FGH=/_GHE=90^0
Therefore, EFGH is a square
Topper's Solved these Questions
Similar Questions
In a ABC,EandF are the mid-points of ACandAB respectively. The altitude AP to BC intersects FE at Q Prove that AQ=QP
View SolutionABCD is a parallelogram and EandF are the centroids of triangles ABD and BCD respectively, then EF= (a)AE (b) BE (c) CE (d)DE
View SolutionABC is a triangle. D is a point on AB such that D=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC
View SolutionABCD is a parallelogram. E is a point on BA such that BE=2 EA and F is a point on DC such that DF=2 FC. Prove that AE CF is a parallelogram whose area is one third of the area of parallelogram AB CD.
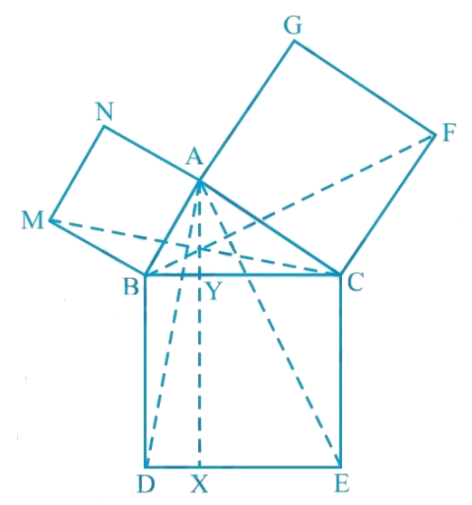
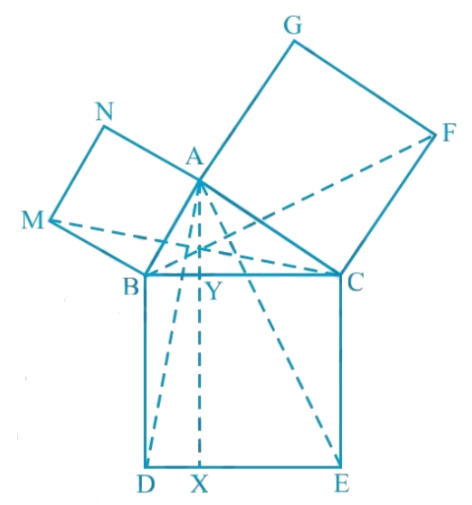
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (CYXE)= ar (ACFG)
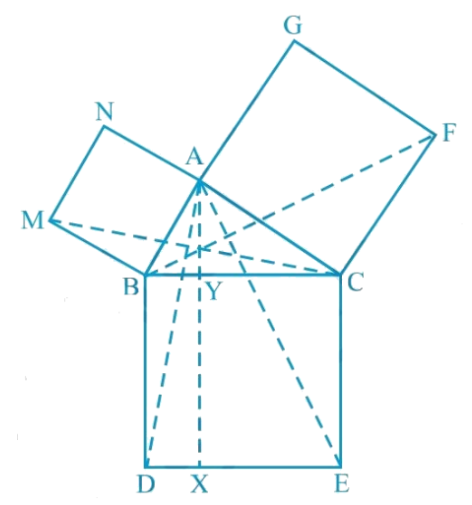 View Solution
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar(CYXE)=ar (ACFG)
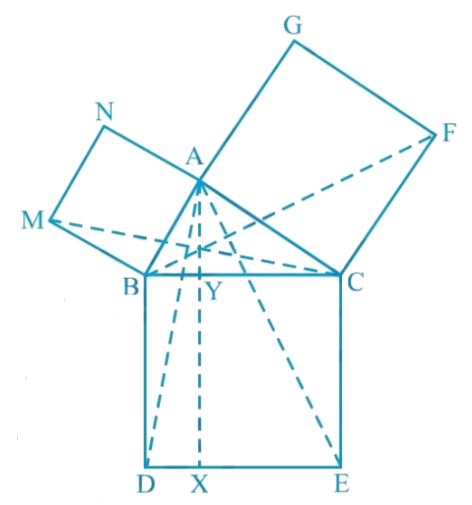 View Solution
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: FCB≅ ACE
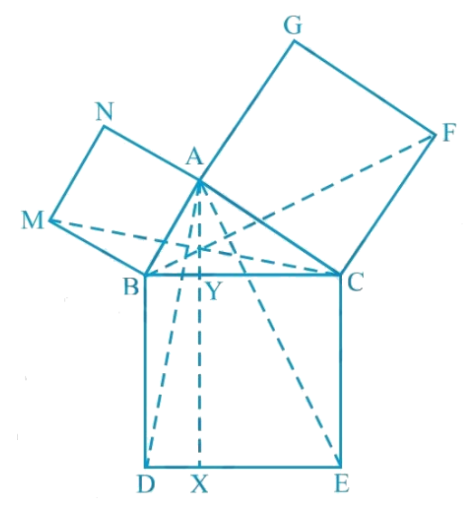 View Solution
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (CYXE)=2ar( FCB)
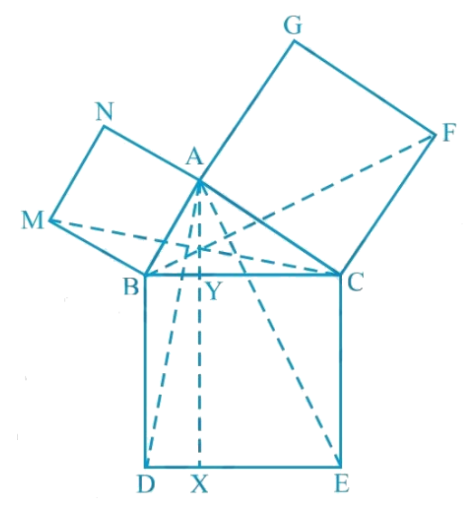 View Solution
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (BYXD)=ar (ABMN)
 View Solution
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (BYXD)=2 ar ( MBC)
 View Solution
View Solution

