AB is a diameter of a circle. P is a point on the semi-circle APB.AHandBK are perpendiculars from AandB respectively to the tangent at P. Prove that AH+BK=AB.
∠MPO=90∘
As BK⊥HM,AH⊥HMandOP⊥HM
So, AH|OP|BK
Assume AH=x,BK=yandOP=rBM=z.
In △MKBand△MHA
∠MKB=∠MHA=90∘
∠BMK=∠AMH
By AA criterion of similarity,
△MKB~△MHA
⇒BKAH=MBMA
⇒yx
=z2r+z
⇒2ry+yz=zx
⇒z=2ryx−y ……..(1)
In△MKBand△MPO,
∠MKB=∠MPO=90∘
∠BMK=∠OMP
By AA criterion of similarly,
△MKB~△MPO
⇒BKOP=BMOM
⇒yr=zr+z
⇒ry+yz=rz
⇒z=ryr−y …… (2)
From equation (1) and (2),
ryr−y=2ryx−y
⇒2r−2y=x−y
⇒2r=x+y
⇒AB=AH+BK
Topper's Solved these Questions
Similar Questions
AB is a diameter of a circle. P is a point on the semi-circle APB.AHandBK are perpendiculars from AandB respectively to the tangent at P. Prove that AH+BK=AB.
View SolutionAB is a diameter of a circle. AHandBK are perpendiculars from A and B respectively to the tangent at P Prove that AH+BK=AB.
View Solution
Knowledge Check
AB is a diameter of the circle x2+y2=4. If p1 and p2 be the lengths of perpendiculars from A and B on the line x+y=1, then maximum value of p1p2 is:
A1/2B7/2C1D2PA and PB are two tangents to a circle with centre O, from a point P outside the circle . A and B are point P outside the circle . A and B are point on the circle . If ∠PAB=47∘ , then ∠OAB is equal to :
A43∘B53∘C50∘D20∘T is a point on the common tangents at P of two circles and if TA and TB are respectively the other tangents at A and B to the two circles drawn from the point T then
ATA=2TBBTA=TBCTA=12TBD3TA=TB
If P is a point on the circle with AB as a diameter, where A and B are (0, 2) and (2,4) respectively, then the locus of P is ____
View SolutionSeg AB is a diameter of a circle with centre P. Seg AC is a chord. A secant through P and parallel to seg AC intersects the tangent drawn at C in D. Prove that line DB is a tangent to the circle.
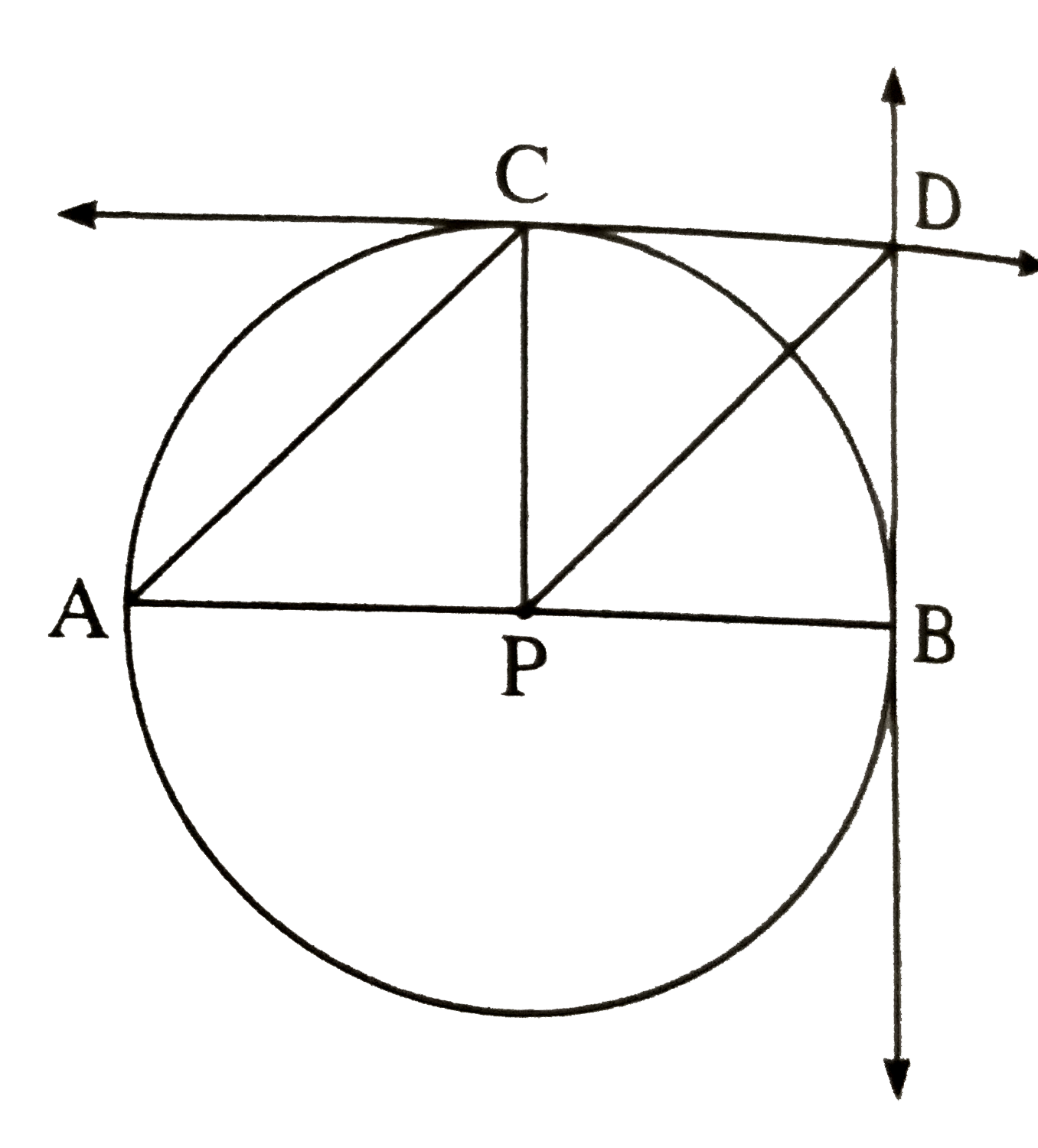
View SolutionTwo circle intersect in AandBandACandAD are respectively the diameters of the circles. Prove that C,B,D are collinear.
View SolutionA point P is 13 xm from the centre of a circle . Radius of the circle is 5 cm . A tangent is drawn from point P to the circle , then the length of the tangent is :
View SolutionQ is a point on the auxiliary circle of an ellipse. P is the corresponding point on ellipse. N is the foot of perpendicular from focus S, to the tangent of auxiliary circle at Q. Then
View Solution
