The radius of the incircle of a triangle is 4 cm and the segments into which one side is divided by the point of contact are 6 cm and 8 cm. Determine the other two sides of the triangle.
To find the other two sides of the triangle given the radius of the incircle and the segments into which one side is divided, we can follow these steps:
1. Identify Given Information:
- Radius of the incircle (r) = 4 cm.
- One side (AC) is divided into two segments: AM = 6 cm and MC = 8 cm.
2. Determine the Length of Side AC:
- Since AM + MC = AC, we have:
AC=AM+MC=6cm+8cm=14cm
3. Use the Tangent Segment Property:
- Let the sides of the triangle be denoted as:
- AB = c
- BC = a
- AC = b (which we found to be 14 cm)
- According to the tangent segment property, if we denote:
- AN = AM = 6 cm (tangent from A)
- CL = MC = 8 cm (tangent from C)
- Let BN = BL = x (tangent from B)
- Thus, we have:
- AB = c = AN + BN = 6 + x
- BC = a = BL + CL = x + 8
4. Calculate the Semi-perimeter (s):
- The semi-perimeter s of the triangle is given by:
s=a+b+c2=(x+8)+14+(6+x)2=2x+282=x+14
5. Use the Area Formula:
- The area A of the triangle can be expressed using the radius of the incircle:
A=r⋅s=4⋅(x+14)
- The area can also be calculated using Heron's formula:
A=√s(s−a)(s−b)(s−c)
- Substituting the values:
- s−a=(x+14)−(x+8)=6
- s−b=(x+14)−14=x
- s−c=(x+14)−(6+x)=8
- Thus, we have:
A=√(x+14)⋅6⋅x⋅8
6. Equate the Two Area Expressions:
- Setting the two expressions for area equal:
4(x+14)=√(x+14)⋅6⋅x⋅8
7. Square Both Sides:
- Squaring both sides to eliminate the square root gives:
16(x+14)2=(x+14)⋅48x
- If x+14≠0, we can divide both sides by x+14:
16(x+14)=48x
8. Solve for x:
- Rearranging gives:
16x+224=48x⟹32x=224⟹x=7
9. Find the Lengths of the Other Two Sides:
- Now substituting x=7:
- AB = c = 6 + x = 6 + 7 = 13 cm
- BC = a = x + 8 = 7 + 8 = 15 cm
Conclusion:
The lengths of the sides of the triangle are:
- AB = 13 cm
- AC = 14 cm
- BC = 15 cm
- Radius of the incircle (r) = 4 cm.
- One side (AC) is divided into two segments: AM = 6 cm and MC = 8 cm.
- Since AM + MC = AC, we have:
AC=AM+MC=6cm+8cm=14cm
- Let the sides of the triangle be denoted as:
- AB = c
- BC = a
- AC = b (which we found to be 14 cm)
- According to the tangent segment property, if we denote:
- AN = AM = 6 cm (tangent from A)
- CL = MC = 8 cm (tangent from C)
- Let BN = BL = x (tangent from B)
- Thus, we have:
- AB = c = AN + BN = 6 + x
- BC = a = BL + CL = x + 8
- The semi-perimeter s of the triangle is given by:
s=a+b+c2=(x+8)+14+(6+x)2=2x+282=x+14
- The area A of the triangle can be expressed using the radius of the incircle:
A=r⋅s=4⋅(x+14)
- The area can also be calculated using Heron's formula:
A=√s(s−a)(s−b)(s−c)
- Substituting the values:
- s−a=(x+14)−(x+8)=6
- s−b=(x+14)−14=x
- s−c=(x+14)−(6+x)=8
- Thus, we have:
A=√(x+14)⋅6⋅x⋅8
- Setting the two expressions for area equal:
4(x+14)=√(x+14)⋅6⋅x⋅8
- Squaring both sides to eliminate the square root gives:
16(x+14)2=(x+14)⋅48x
- If x+14≠0, we can divide both sides by x+14:
16(x+14)=48x
- Rearranging gives:
16x+224=48x⟹32x=224⟹x=7
- Now substituting x=7:
- AB = c = 6 + x = 6 + 7 = 13 cm
- BC = a = x + 8 = 7 + 8 = 15 cm
The lengths of the sides of the triangle are:
- AB = 13 cm
- AC = 14 cm
- BC = 15 cm
Topper's Solved these Questions
Similar Questions
The radius of the incircle of a triangle is 4 cm and the segments into which one side is divided by the point of contact are 6 cm and 8 cm. Determine the other two sides of the triangle.
View SolutionQ25. Infig.,a triangle ABC is drawn to a circle of radius 3 cm, such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 6 cm and 8cm respect Find the side AB if the area of ΔABC=63cm2
View Solution
Knowledge Check
The radius of the incircle of triangle when sides are 18, 24 and 30 cms is
A2 cmB4 cmC6 cmD9 cmThe radius of the incircle of a triangle whose sides are 9 cm, 12 cm and 15 cm is
A9 cmB13 cmC3 cmD6 cmThe radius of the incircle of the equilateral triangle having each side 6 cm is
AA)2√3 cmBB)√3 cmCC)6√3 cmDD)2cm
A triangle ABC is drawn to circumscribe a circle of radius 4cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 6cm and 8cm respectively. Find the lengths of the sides AB and AC.
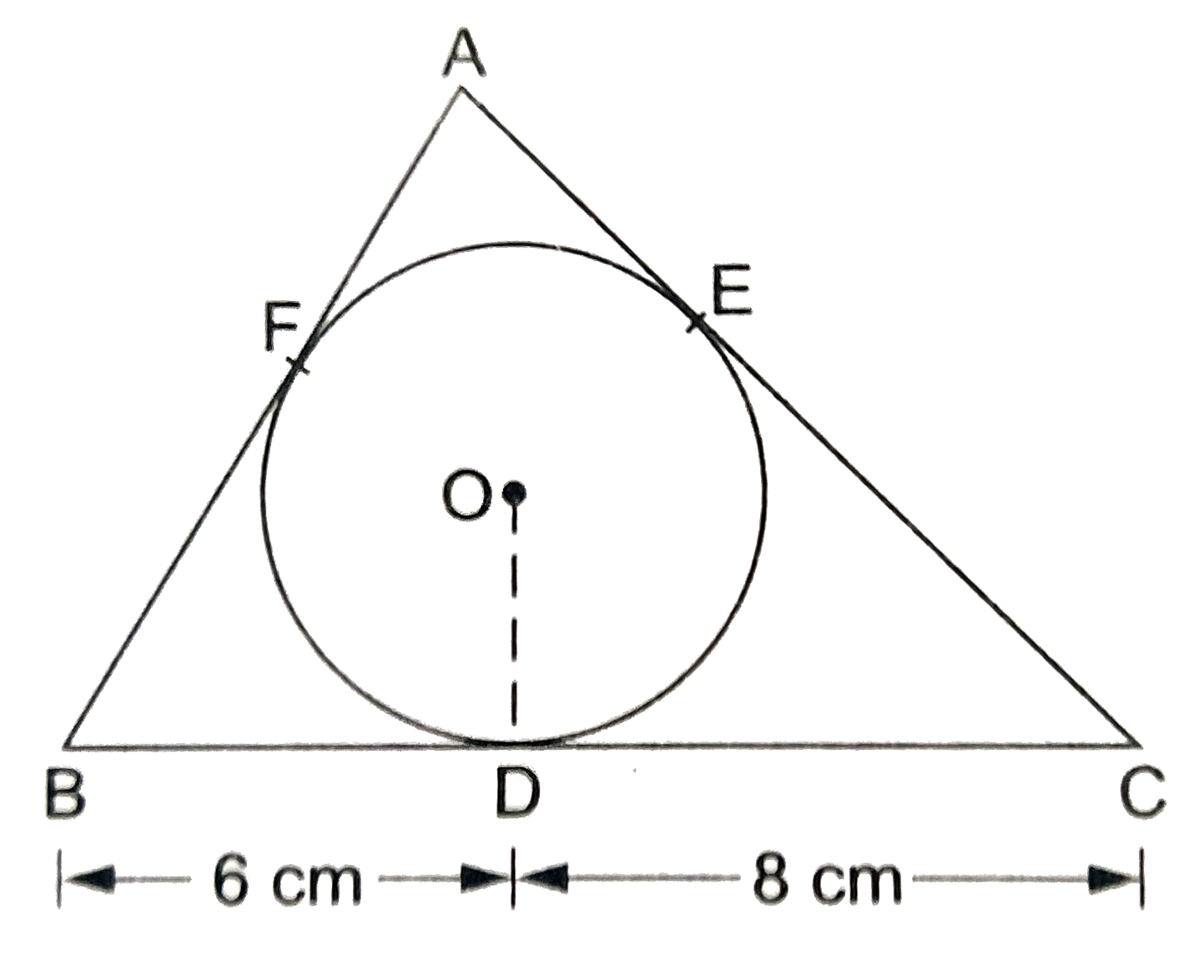
View SolutionIn the given figure ΔABC is drawn to circumscribe a circle of radius 3 cm, such that the segment BD and DC into which BC is divided by the point of contact D are of length 6 cm and 8 cm respectively, find side AB if the ar (ΔABC)=63cm2
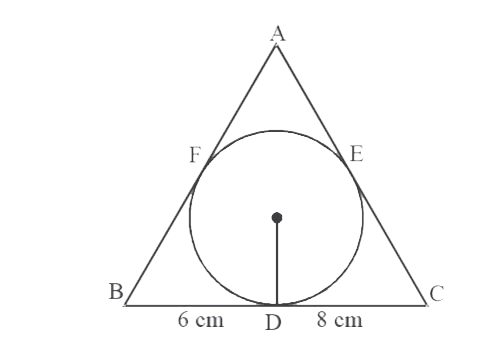
View SolutionIn Figure 5, a triangle PQR is drawn to circumscribe a circle of radius 6 cm such that the segments QT and TR into which QR is divided by the point of contact T, are of lengths 12 cm and 9 cm respectively. If the area of ΔPQR=189cm2, then find the lengths of sides PQ and PR.
View SolutionArea of the incircle of an equilateral triangle with side 6 cm is
View SolutionThe radius of the circumcircle of a right angled triangle is 15 cm and the radius of its inscribed circle is 6 cm. Find the sides of the triangle.
View Solution
