AB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
Let M be the midpoint of AB. Then, l⊥AB and passes through M. Let P be a given point on l.
Then, we have to show that PA = PB.
In ΔPMAandΔPMB, we have
MA=MB [∵ M is the midpoint of AB],
∠PMA=∠PMB=90∘ (given)
and PM = PM (common).
∴ ΔPMA~ΔPMB (by SAS-criteria)
Hence, PA=PB (c.p.c.t).
The shows that P is equidistant from A and B.
Similar Questions
AB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View SolutionAB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View SolutionA line segment is symmetrical about its perpendicular bisector.True or false?
View SolutionTo construct the perpendicular bisector of a given line segment.
View SolutionDraw perpendicular bisector to line segment AB if l(AB)=7cm.
View SolutionIn the given figure, AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B. Show that the line PQ is the perpendicular bisector of AB.
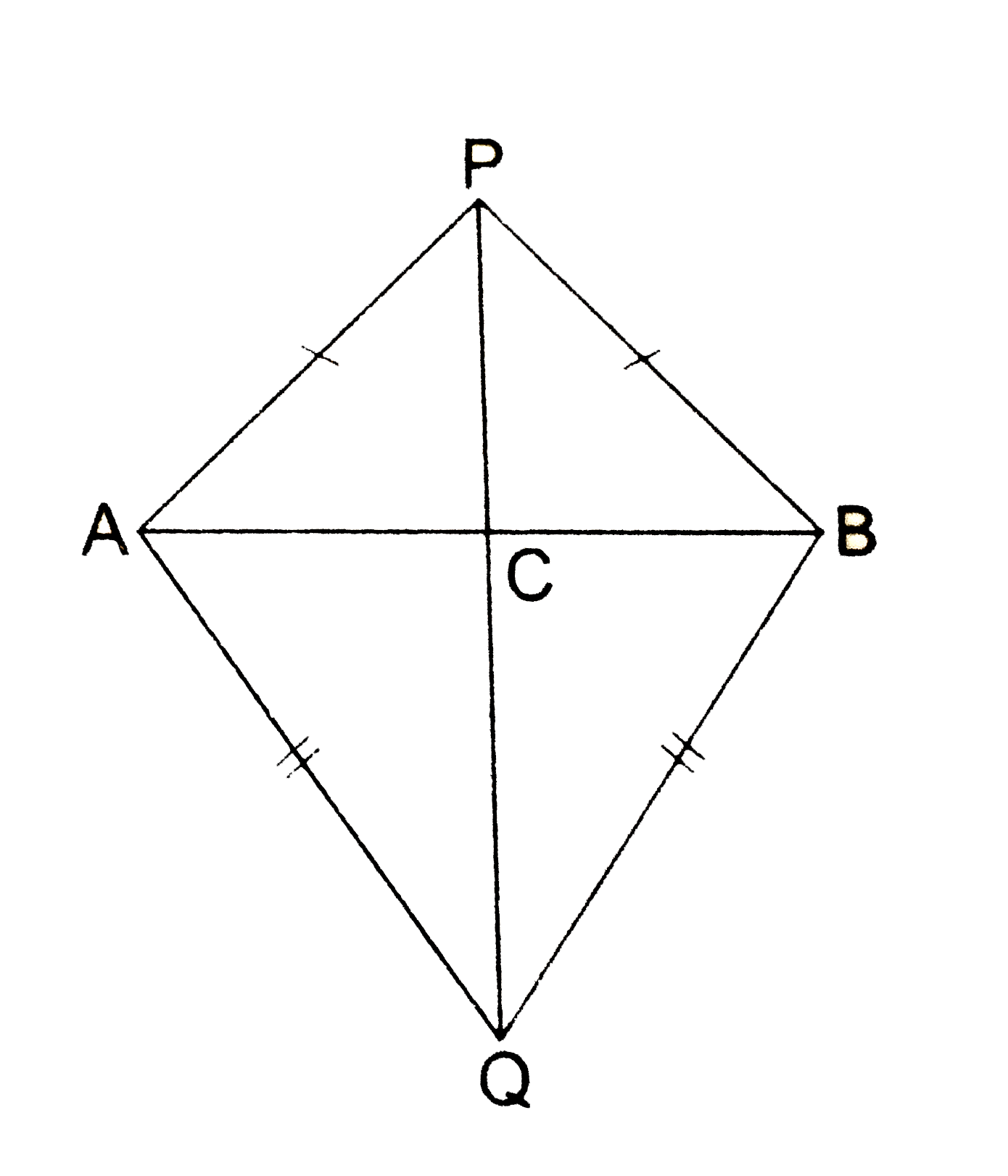
View SolutionAB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (in figure). Show that the line PQ is perpendicular bisector of AB
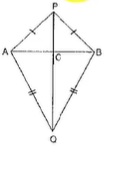
View SolutionTwo chords AB and CD of a circle are parallel and a line l is the perpendicular bisector of AB. Show that l bisects CD
View SolutionTwo chords AB and CD of a circle are parallel and a line l is the perpendicular bisector of AB . Show that l bisects CD.
View SolutionAB is a line-segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (see Fig. 7.37). Show that the line PQ is the perpendicular bisector of AB
View Solution
