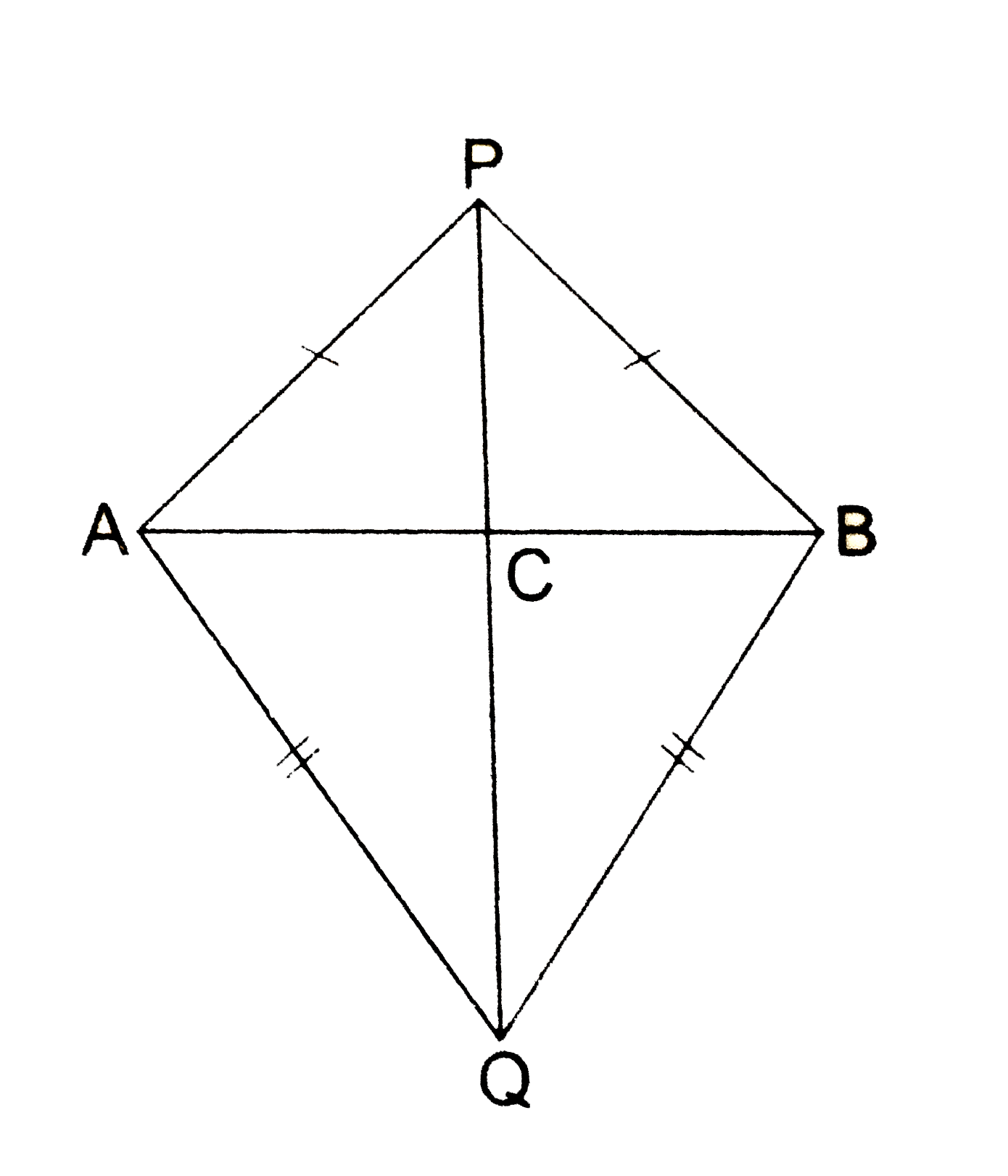
AB is a line-segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (see Fig. 7.37). Show that the line PQ is the perpendicular bisector of AB
In∠APQand∠BPQ
PA=PB
QA=QB
PQ=PQ
∠APQ≅∠BPQ(SSS)
∠APQ=∠BPQ
∠AQP=∠BQP
∠PAQ=∠PBQ
In ∠APCand∠BPC
∠APC=∠BPL
∠PAC=∠PBC
AP=BP
∠APC≅∠BPC (ASA)
∠PCA=∠PCB
AC=BC(C is Mid point of AB)
∠PCA+∠PCB=1800
2∠PCA=1800
∠PCA=900
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.46videos
TRIANGLES
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.18videos
TRIANGLES
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.28videos
TRIANGLES
- BOOK - NCERTCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - EXERCISE 13.810videos
SURFACE AREAS AND VOLUMES
Similar Questions
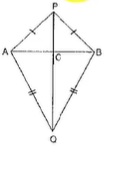
In the given figure, AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B. Show that the line PQ is the perpendicular bisector of AB.
 View Solution
View SolutionAB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (in figure). Show that the line PQ is perpendicular bisector of AB
 View Solution
View SolutionAB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View SolutionAB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View SolutionShow that the locus of a point, equidistant from the endpoints of a line segment, is the perpendicular bisector of the segment
View SolutionShow that the locus of a point, equidistant from the endpoints of a line segment, is the perpendicular bisector of the segment
View SolutionP is a point equidistant from two lines l and m intersecting at point A(see Fig. 7.38). Show that the line AP bisects the angle between them.
View SolutionDraw a line segment AB=5.6cm. Draw the perpendicular bisector of AB.
View SolutionDraw a line segment AB of length 4.8 cm. Draw the perpendicular bisector of seg AB
View SolutionIf a number of circles pass through the end points P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ.
View Solution

