A binomial random variable X, 5P(X = 3) = 2P(X = 2), when n = 5. Find the value of parameter p.
The correct Answer is:p=27
To solve the problem, we need to find the value of the parameter p in a binomial distribution where n=5 and the relationship between the probabilities of X=3 and X=2 is given by 5P(X=3)=2P(X=2).
1. Understand the Binomial Probability Formula:
The probability of getting exactly k successes in n trials is given by:
P(X=k)=(nk)pk(1−p)n−k
where (nk) is the binomial coefficient.
2. Set Up the Probabilities:
For n=5:
- Calculate P(X=3):
P(X=3)=(53)p3(1−p)2
- Calculate P(X=2):
P(X=2)=(52)p2(1−p)3
3. Substitute the Binomial Coefficients:
- The binomial coefficients are:
(53)=5!3!(5−3)!=5×42×1=10
(52)=5!2!(5−2)!=5×42×1=10
Thus, we have:
P(X=3)=10p3(1−p)2
P(X=2)=10p2(1−p)3
4. Set Up the Given Equation:
According to the problem:
5P(X=3)=2P(X=2)
Substituting the probabilities:
5(10p3(1−p)2)=2(10p2(1−p)3
Simplifying gives:
50p3(1−p)2=20p2(1−p)3
5. Cancel Common Terms:
Assuming p≠0 and 1−p≠0, we can divide both sides by 10p2(1−p)2:
5p=2(1−p)
6. Rearranging the Equation:
Expanding and rearranging gives:
5p=2−2p
5p+2p=2
7p=2
7. Solve for p:
p=27
Final Answer:
The value of the parameter p is 27.
The probability of getting exactly k successes in n trials is given by:
P(X=k)=(nk)pk(1−p)n−k
where (nk) is the binomial coefficient.
For n=5:
- Calculate P(X=3):
P(X=3)=(53)p3(1−p)2
- Calculate P(X=2):
P(X=2)=(52)p2(1−p)3
- The binomial coefficients are:
(53)=5!3!(5−3)!=5×42×1=10
(52)=5!2!(5−2)!=5×42×1=10
P(X=3)=10p3(1−p)2
P(X=2)=10p2(1−p)3
According to the problem:
5P(X=3)=2P(X=2)
Substituting the probabilities:
5(10p3(1−p)2)=2(10p2(1−p)3
Simplifying gives:
50p3(1−p)2=20p2(1−p)3
Assuming p≠0 and 1−p≠0, we can divide both sides by 10p2(1−p)2:
5p=2(1−p)
Expanding and rearranging gives:
5p=2−2p
5p+2p=2
7p=2
p=27
The value of the parameter p is 27.
Topper's Solved these Questions
- MODEL TEST PAPER-12 BOOK - ICSECHAPTER - MODEL TEST PAPER-12 EXERCISE - SECTION-B
10 Videos
- MODEL TEST PAPER-12 BOOK - ICSECHAPTER - MODEL TEST PAPER-12 EXERCISE - SECTION-C
10 Videos
- MODEL TEST PAPER-11BOOK - ICSECHAPTER - MODEL TEST PAPER-11EXERCISE - SECTION-C
9 Videos
- MODEL TEST PAPER-16BOOK - ICSECHAPTER - MODEL TEST PAPER-16EXERCISE - SECTION -C (65 MARKS)
10 Videos
Similar Questions
Knowledge Check
For a binomial variate X , if n = 3 and P(X =1) = 12 P(X =3) , then the value of p is
A12B13C23D25For a binomial variate X , if n = 3 and 4P (X=1) = 3P (X=3) , then p (probability of success)
AA) 15BB) 35CC) 13DD) 23
For a binomial variate X with n=6, if P(X=2)=9P(X=4), then its variance is
View SolutionIf X is a binomial variate with n = 7 and P(X=3)=P(X=4) then P(X=5)=
View SolutionThe probability distribution of a random variable X is given below
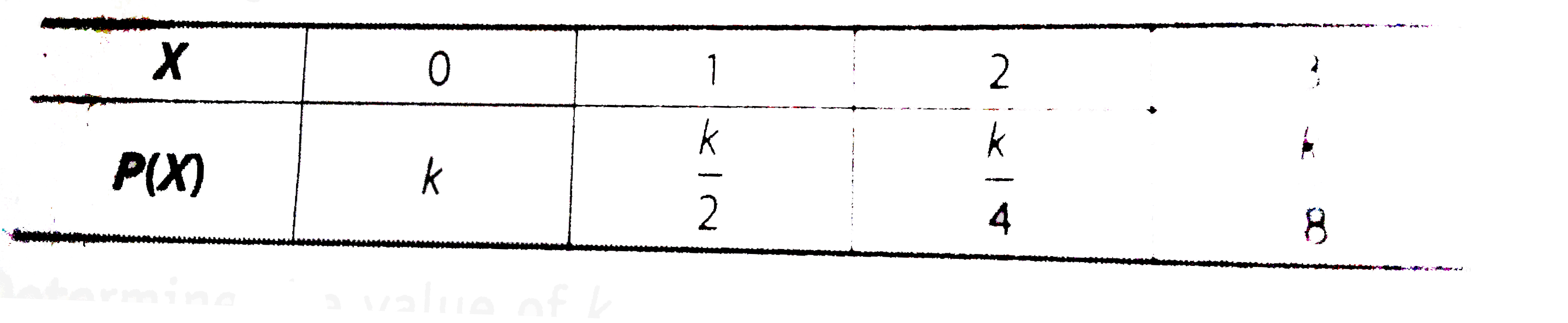
(i) Determine the value of K .
(ii) Determine P(X≤2)andP(X>2).
(iii) Find P(X≤2)+P(X>2).
View SolutionIf .nP5=20.nP3, find the value of n.
View SolutionThe random variable X can take only the values 0,1,2. Given that P(X=0)=P(X=1)=p and that E(X2)=E(X); find the value of p.
View SolutionThe random variable X can take only the values 0, 1, 2. Given that P(X=0) = P(X= 1) = p and E(X2)=E(X) , then find the value of p
View Solution

