A circle circumscribing an equilateral triangle with centroid at $(0, 0)$ of a side a isdrawn and a square is drawn touching its four sides to circle. The equation ofcircle circumscribing the square is :

A

$x^{2} + y^{2} = 2 a^{2}$

B

$3 x^{2} + 3 y^{2} = 2 a^{2}$

C

$5 x^{2} + 5 y^{2} = 3 a^{2}$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Clearly, centre of the circumcircle is at the origin and radius is two-third of the altitude $\frac{\sqrt{3}}{2}$ a. So, the equation of the circumcircle is
$x^{2} + y^{2} = {(\frac{a}{\sqrt{3}})}^{2}$

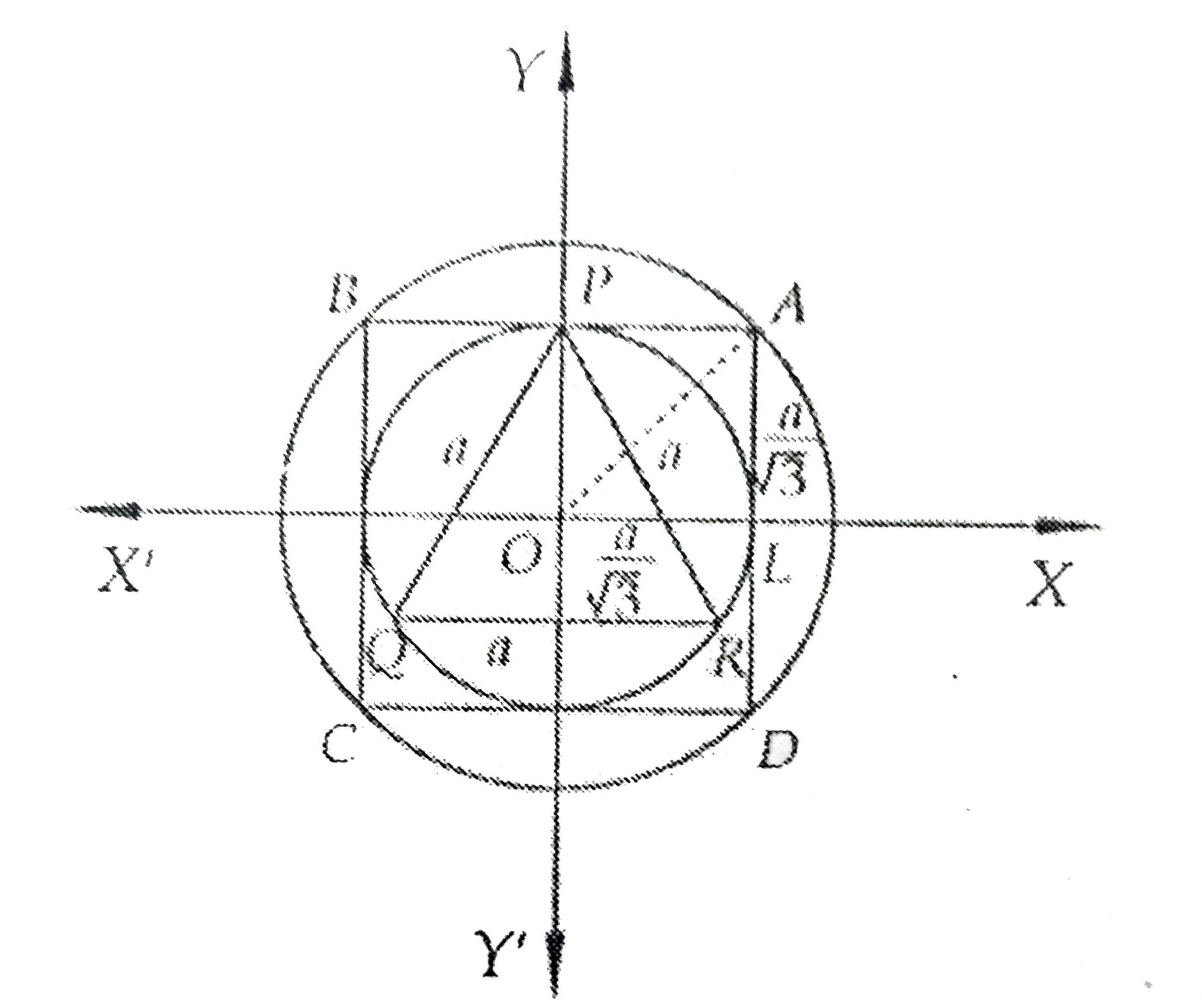
Clearly, Radius of the circumcircle of the square ABCD
$= O A = \sqrt{O L^{2} + A L^{2}} = \sqrt{\frac{a^{2}}{3} + \frac{a^{2}}{3}} = \sqrt{\frac{2}{3}} a$
So, the equation of the circumcircle is
$x^{2} + y^{2} = \frac{2}{3} a^{2} \Rightarrow 3 (x^{2} + y^{2}) = 2 a^{2}$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A circle is inscribed in an equilateral triangle of side a. What is the area of any square inscribed in the circle ?
A $\frac{a^{2}}{3}$
B $\frac{a^{2}}{4}$
C $\frac{a^{2}}{6}$
D $\frac{a^{2}}{8}$
Question 2 - Select One
A circle is cirumscribed in an equilateral triangle of side $' l'$ . The area of any square inscribed in the circle is :
A $\frac{4}{3} l^{2}$
B $\frac{2}{3} l^{2}$
C $\frac{1}{3} l^{2}$
D $l^{2}$
Question 3 - Select One
A circle is inscribed in a equilateral triangle of side 24 cm. What is the area ( in $c m^{2}$ ) of a square inscribed in the circle ?
A48
B72
C54
D96

OBJECTIVE RD SHARMA-CIRCLES-Section I - Solved Mcqs

Home
Ask Doubt
Profile