A circle has radius √2cm it is divided into 2 segments by a chord of length 2cm prove that angle subtended by the chord at a point in major segment is 45∘
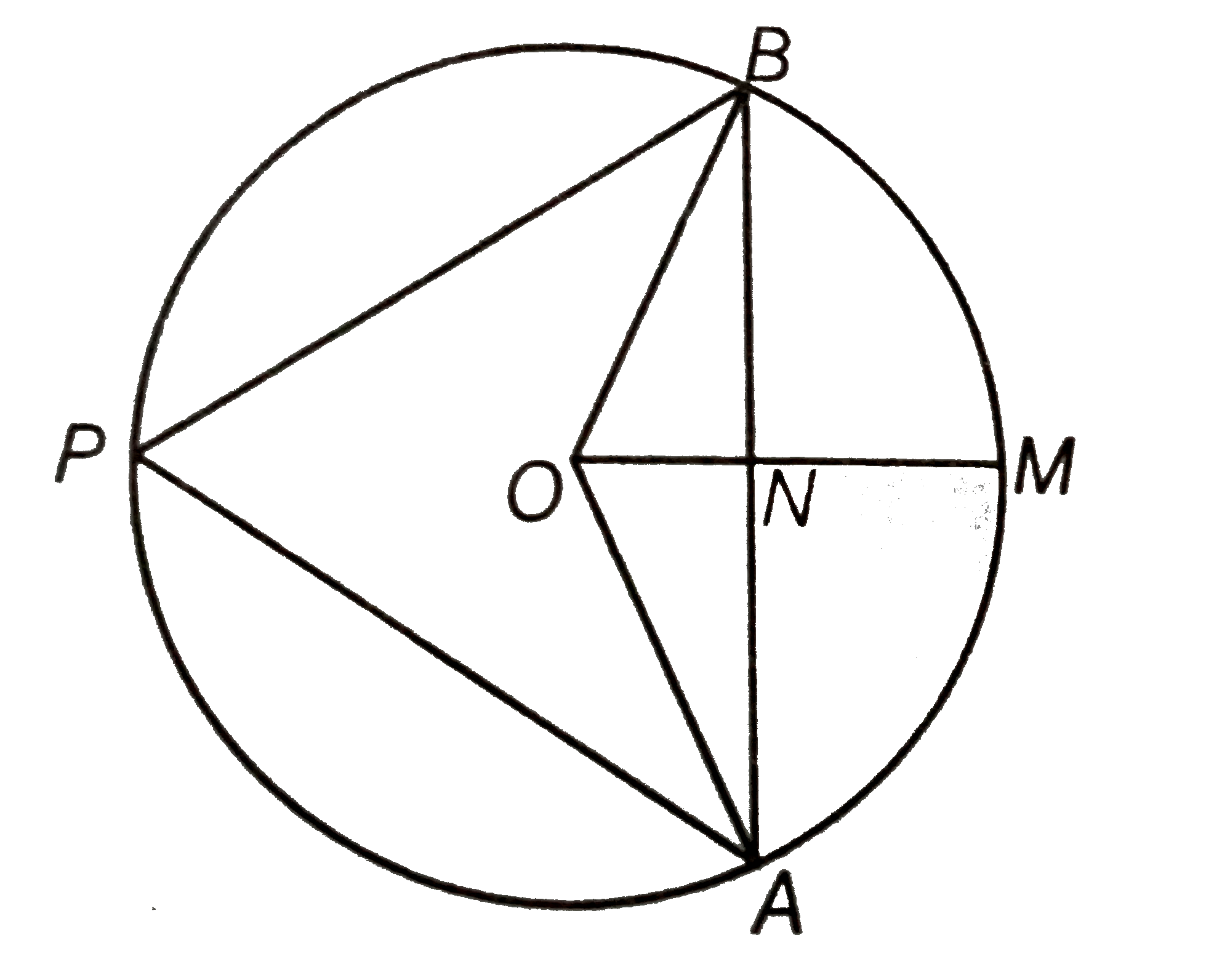
Draw a circle having centre O. Let AB=2 cm be a chord of a circle. A chord AB is divided by the line OM in two equal segments.
To prove ∠APB=45∘
Here, AN=NB = 1 cm
and OB=√2cm
In ΔONB,OB2=ON2+NB2
[use Pythagoras theorem]
⇒(√2)2=ON2+(1)2
⇒ON2=2−1=1
⇒ON=1cm
[taking positive square root, because distance is always positive]
Also, ∠ONB=90∘ [ON is the perpendicular bisector of the chord AB]
∴∠NOB=∠NBO=45∘
Similarly, ∠AON=45∘
Now, ∠AOB=∠AON+∠NOB
=45∘+45∘=90∘
We know that, chord subtends an angle to the circle is half the angle subtended by it to the centre.
∴∠APB=12∠AOB
=90∘2=45∘
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles
34 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
A circle has radius √2cm it is divided into 2 segments by a chord of length 2cm prove that angle subtended by the chord at a point in major segment is 45∘
View SolutionConsider the following statements :
1. If non-parallel sides of a trapezium are equal, then it is cyclic.
2. If the chord of a circle is equal to its radius, then the angle subtended by this chord at a point in major segment is 30∘.
Which of the above statements is/are correct?
View Solution
Knowledge Check
If the chord of a circle is equal to the radius of the circle, then the angle subtended by the chord at a point on the minor arc is:
A120∘B150∘C100∘D110∘A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc
A150∘B180∘C160∘D170∘
A chord of a circle is equal to its radius. The angle subtended by this chord at a point on the circumference is
View SolutionThe chord of a circle is equal to its radius, find the angle subtended by this chord at the centre.
View SolutionA chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
View SolutionA chord of a circle is equal to the radius of the circle find the angle subtended by the chord at a point on the monor arc and also at a point on the major arc.
View SolutionDraw a chord of length 6 cm in a circle of radius 4 cm and shade the major segment.
View Solutionx−y+b=0 is a chord of the circle x2+y2=a2 subtending an angle 600 in the major segment of the circle. Statement 1 : ba=±√2. Statement 2 : The angle subtended by a chord of a circle at the centre is twice the angle subtended by it at any point on the circumference. (A) Both 1 and 2 are true and 2 is the correct explanation of 1 (B) Both 1 and 2 are true and 2 is not a correct explanation of 1 (C) 1 is true but 2 is false (D) 1 is false but 2 is true
View Solution
