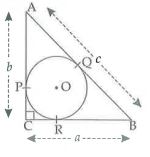
A circle having centre as O' and radius r' touches the incircle of $Δ A B C$ externally at. F, where F is on BC and also touches its circumcircle internally at G. It O is the circumcentre of $Δ A B C$ and I is its incentre, then Solution in Bengali

A

OO'=R-r'

B

Perpendicular distance from O to line joining IO' is $∣ ∣ ∣ \frac{b - c}{2} ∣ ∣ ∣$

C

Projection of OO' on line joining IO'=r'+R cos A

D

$r' = \frac{Δ}{a} {tan}^{2} A$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

From figure, OO' = OG - O'G = R-r'

$O E = D E = | B F - B D | = ∣ ∣ ∣ s - b - \frac{a}{2} ∣ ∣ ∣ = \frac{| c - b |}{2}$
OD = EF = R cos A
From $Δ O E O'$ , using Pythagoras theorem, we get
${(R - r')}^{2} = {(R cos A + r')}^{2} + {(\frac{c - b}{2})}^{2}$
$\Rightarrow r' = \frac{b c}{4 R} {tan}^{2} \frac{A}{2}$
$= \frac{Δ}{a} {tan}^{2} \frac{A}{2}$

|

Class 12 MATHS SOLUTIONS AND PROPERTIES OF TRIANGLE

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-SOLUTIONS AND PROPERTIES OF TRIANGLE -Multiple Correct Answers Type

Home
Ask Doubt
Profile