a circle passing through the point (2,2(√2−1)) touches the pair of lines x2−y2−4x+4=0. The centre of the circle is
(2,2√2) and (2,6√6−8)
(2,5√2) and (2,7√2)
(2,5√2−1) and (2,−3)
None of these
The correct Answer is:A
The equation of the pair of lines is
⇒(x−2)2−y2=0
⇒(x−2)=±y
i.e. x−y=2 and x+y=2
The centre of the circle touching the above lines must lie on the angular bisectors of the above lines. Hence, C≡(2,k)
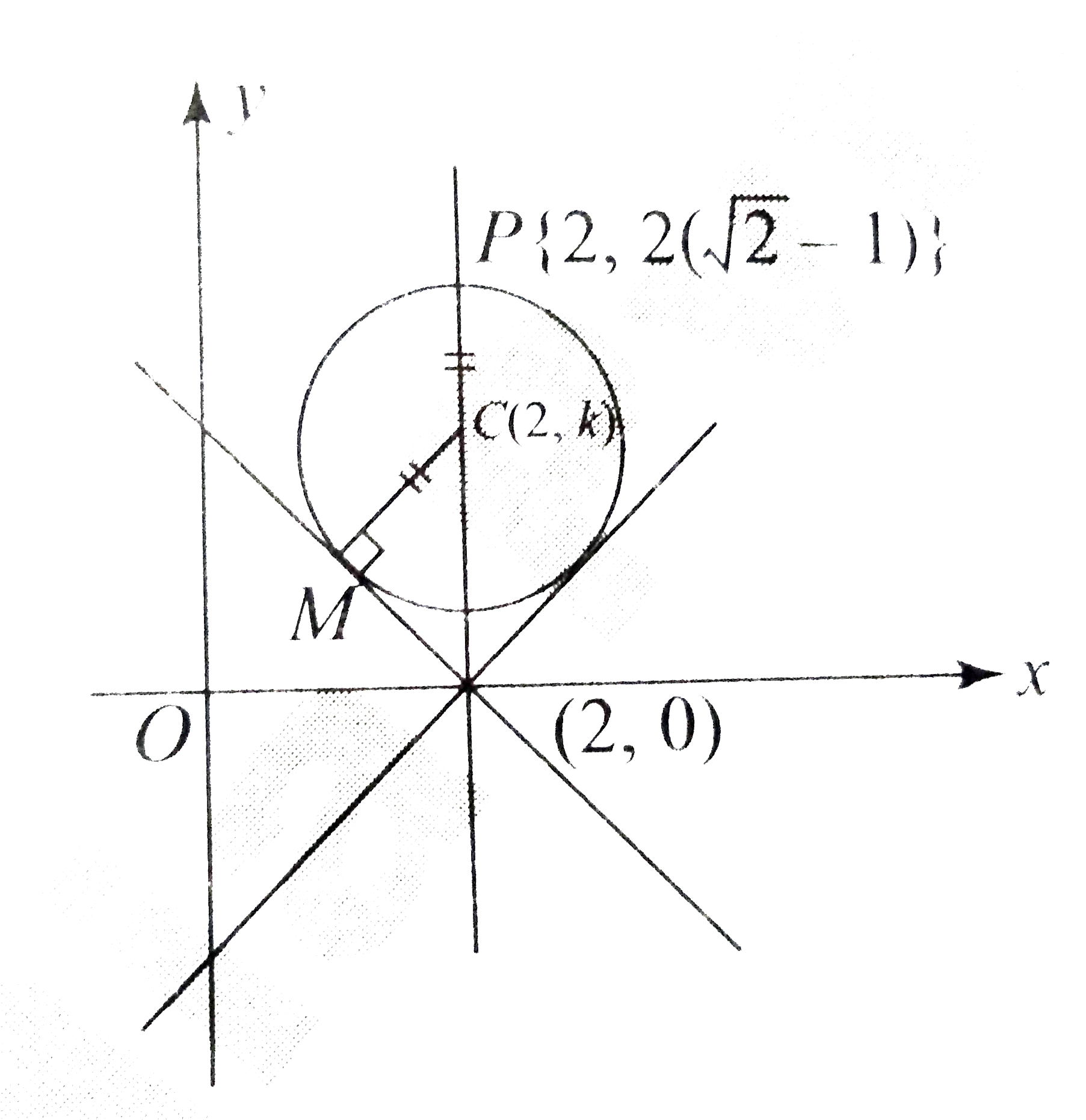
Thus, we have
⇒|2+k−2|√2=2(√2−1)−k
⇒±k√2=2(√2−1)−k
⇒k(1±1√2)=2(√2−1)
⇒k=2√2(√2−1)√2±1
=2√2,2√2(√2−1)2
=2√2,6√2−8
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - JEE Advanced (Single Correct Answer Type)
14 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Question Bank
30 Videos
Similar Questions
a circle passing through the point (2,2(√2−1)) touches the pair of lines x2−y2−4x+4=0. The centre of the circle is
View SolutionA circle passes through point (3,√72) and touches the line-pair x2−y2−2x+1=0. Centre of circle lies inside the circle x2+y2−8x+10y+15=0. Coordinates of centre of circle are given by (A) (4,0) (B) (5,0) (C) (6,0) (D) (0,4)
View Solution
Knowledge Check
If circle C passing through the point (2, 2) touches the circle x2+y2+4x−6y=0 externally at the point (1, 1), then the radius of C is:
A√12B√13C√15D4A variable circle is described to pass through the point (a, 0) and touch the line x+y=0. Locus of the centre of the above circle is
AparabolaBellipseChyperbolaDnone of theseThe equation of the circle passing through the point (-1, 2) and having two diameters along the pair of lines x2−y2−4x+2y+3=0, is
Ax2+y2−4x−2y+5=0Bx2+y2+4x+2y−5=0Cx2+y2−4x−2y−5=0Dnone of these
Lines passing through the point (11,−2) and touching the circle x2+y2=25 are
View SolutionCentre of the circles passing through the point (−4,3) and touching the lines x+y=2 and x−y=2 is
View SolutionA circle passes through a point (2,8) and touches the lines 4x−3y−24=0and4x+3y+42=0 and centre lies on the line x=λ then (−4λ) is
View SolutionIf a circle C passing through the point (4,0) touches the circle x2+y2+4x−6y=12 externally at the point (1,-1) ,then the radius of C is
View SolutionCentre of a circle passing through point (0,1) and touching the curve y=x2 at (2,4) is
View Solution
