P and Q are two points on a line passing through (2, 4) and having slope m. If a line segment AB subtends a right angles at P and Q, where A(0, 0) and B(6,0), then range of values of m is

A

$(\frac{2 - 3 \sqrt{2}}{4}, \frac{2 + 3 \sqrt{2}}{4})$

B

$(- \infty, \frac{2 - 3 \sqrt{2}}{4}) \cup (\frac{2 + 3 \sqrt{2}}{4}, \infty)$

C

$(- 4, 4)$

D

$(- \infty, - 4) \cup (4, \infty)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

AB subtends right angle at P and Q on variable line.

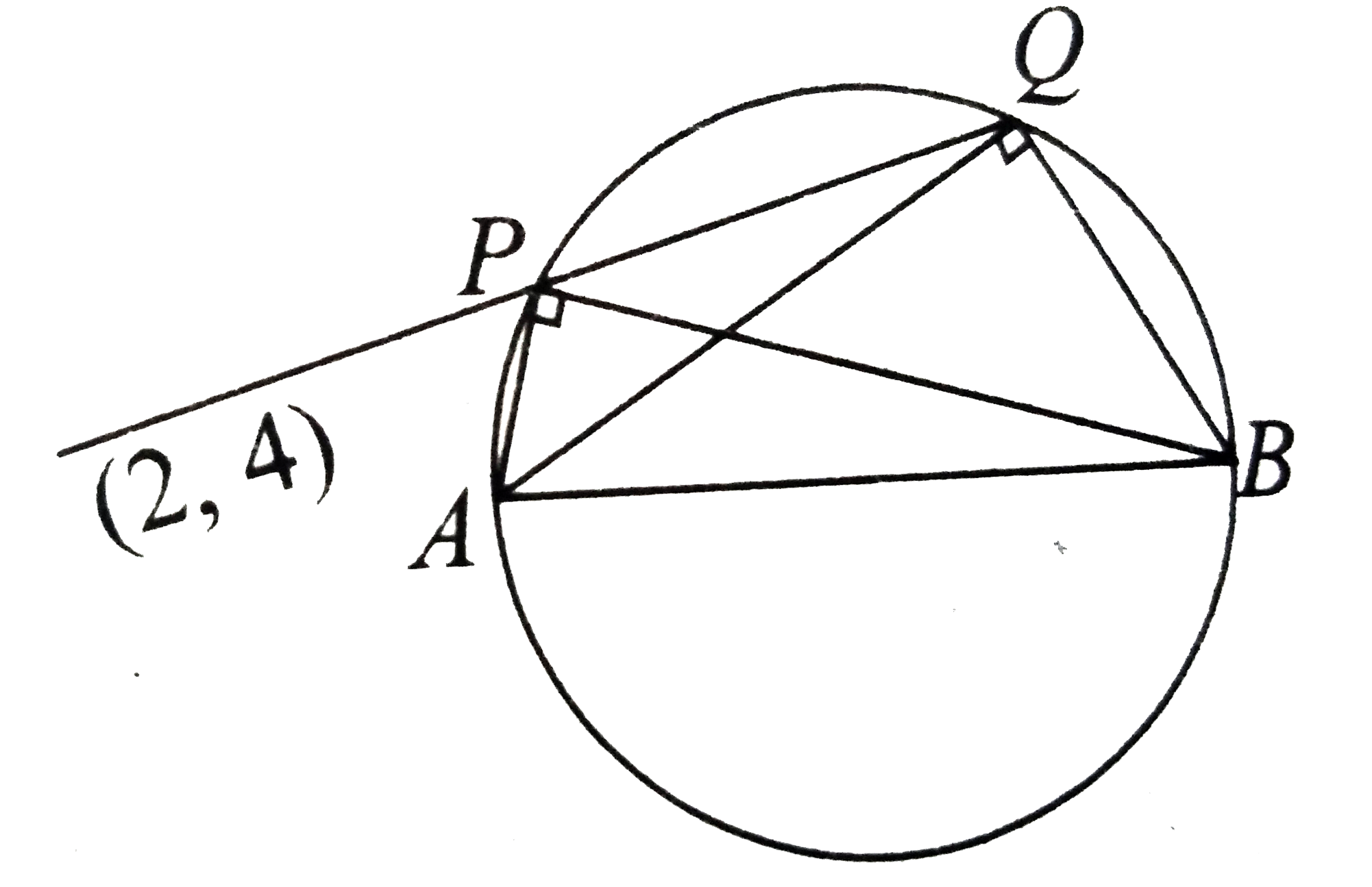
So, AB is a diameter of circle whose chord is a variable line. Equation of circle is:
$x (x - 6) + y \times y = 0$
or $x^{2} + y^{2} - 6 x = 0$ (i)
Equation of line through (2,4) is:
$y - 4 = m (x - 2)$
or $y = m x + (4 - 2 m)$ (ii)
Line (ii) is a chord if $∣ ∣ ∣ \frac{3 m + (4 - 2 m)}{\sqrt{1 + m^{2}}} ∣ ∣ ∣ < 3$
$\Rightarrow 8 m^{2} - 8 m - 7 > 0$
$m \in (- \infty, \frac{2 - 3 \sqrt{2}}{4}) \cup (\frac{2 + 3 \sqrt{2}}{4}, \infty)$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The slope of line passing through the points $P (- 3, 5)$ and $Q (4, - 1)$ is
A $\frac{- 7}{6}$
B $\frac{- 6}{7}$
C $\frac{- 1}{7}$
D $- 2$

CENGAGE-CIRCLES-Single Correct Answer Type

Home
Ask Doubt
Profile