Q.ys In the xy-plane, the length of the shortest path from (0.0) to (12.16) that does not go inside the circle 6) (y-8) 25 is (D) 10 (B) 10 5 (A) 10 Dps' on Circle

A

$10 \sqrt{3}$

B

$10 \sqrt{5}$

C

$10 \sqrt{3} + \frac{5 π}{3}$

D

$10 + 5 π$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Let $O \equiv (0, 0) P \equiv (6, 8)$ and $Q \equiv (12, 16)$ .
As shown in the figure, the shortest route consists of tangent OT, minor arc TR and tangent RQ.
Since $O P = 10, P T = 5$ , and $∠ O T P = 90^{\circ}$ , it follows that $∠ O P T = 60^{\circ}$ and $O T = 5 \sqrt{3}$ .

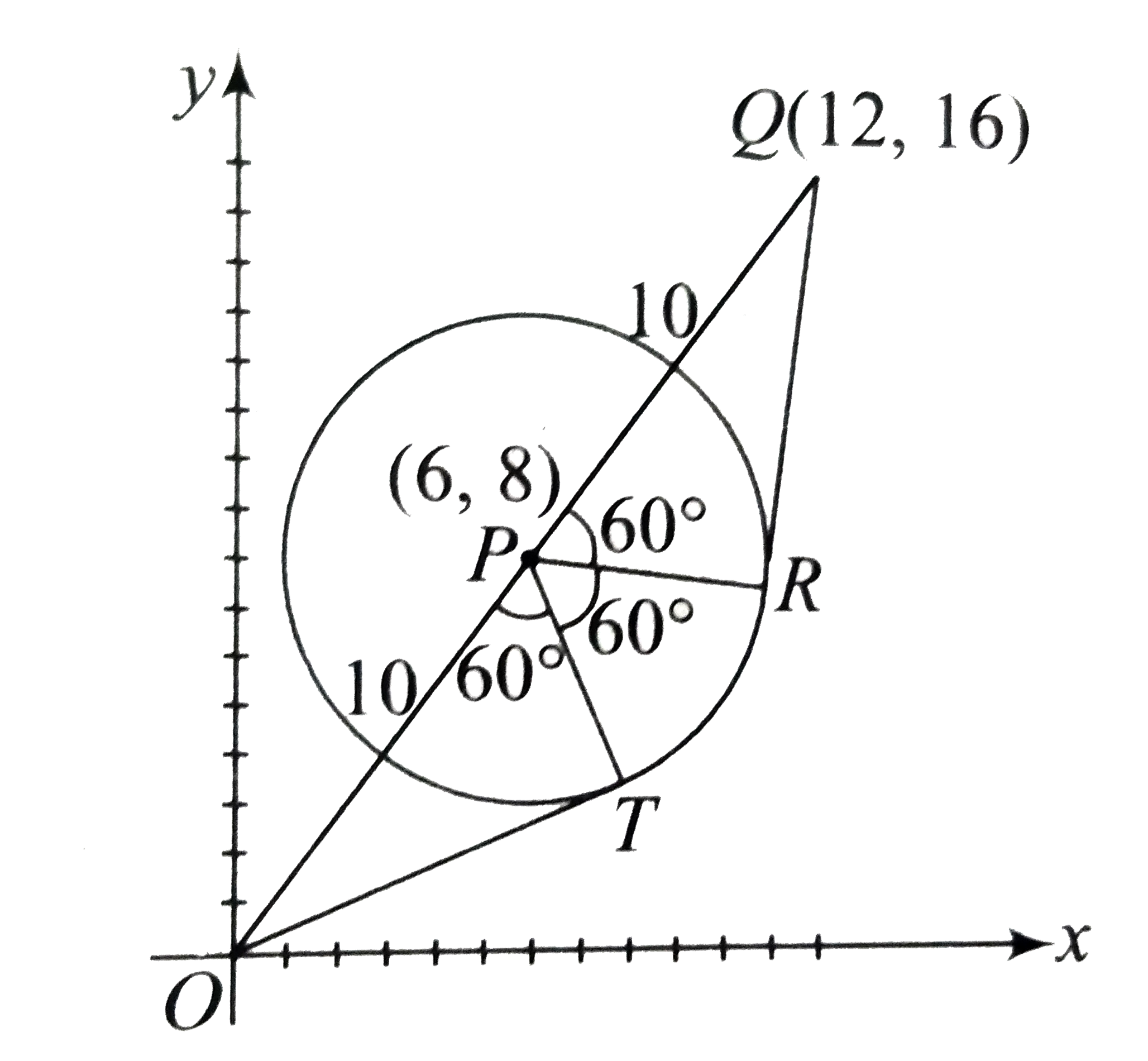
Similarly, $P Q = 10$ and $P R = 5$
$∴ ∠ Q P R = 60^{\circ}$ and $Q R = 5 \sqrt{3}$
Also points O,P and Q are collinear as $m_{O P} = m_{P Q}$
Thus, $∠ R P T = 60^{\circ}$ and arc TR is of length $\frac{5 π}{3}$ .
Hence, the length of the shortest route is $2 (5 \sqrt{3}) + \frac{5 π}{3}$ .

|

Updated on:21/07/2023

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Find the centre of the circle $x^{2} + y^{2} - 8 x + 10 y - 12 = 0$ .
A $(4, - 5)$
B $(- 4, - 5)$
C $(4, 5)$
DNone of these
Question 2 - Select One
The centre of a circle passing through the points (0, 0), (1, 0) and touching the circle $x^{2} + y^{2} = 9$ , is
A $(\frac{3}{2}, \frac{1}{2})$
B $(\frac{1}{2}, \frac{3}{2})$
C $(\frac{1}{2}, \frac{1}{2})$
D $(\frac{1}{2}, - 2^{1 / 2})$
Question 3 - Select One
Find the centre of the circle $x^{2} + y^{2} + 8 x + 10 y - 8 = 0$ .
A $(4, - 5)$
B $(- 4, - 5)$
C $(4, 5)$
DNone of these

CENGAGE-CIRCLES-Single Correct Answer Type

Home
Ask Doubt
Profile