A circle touches both the coordinate axes and the line x−y=√2a,a>0, the coordinates of the centre of the circle cannot be
A
(a, a)
B
(a, -a)
C
(-a, a)
D
(-a, -a)
Video Solution
Text Solution
The correct Answer is:B
Let the radius of the circle be r. Then, coordinates of its centre can be (r, r), (-r, -r) and (r, -r).
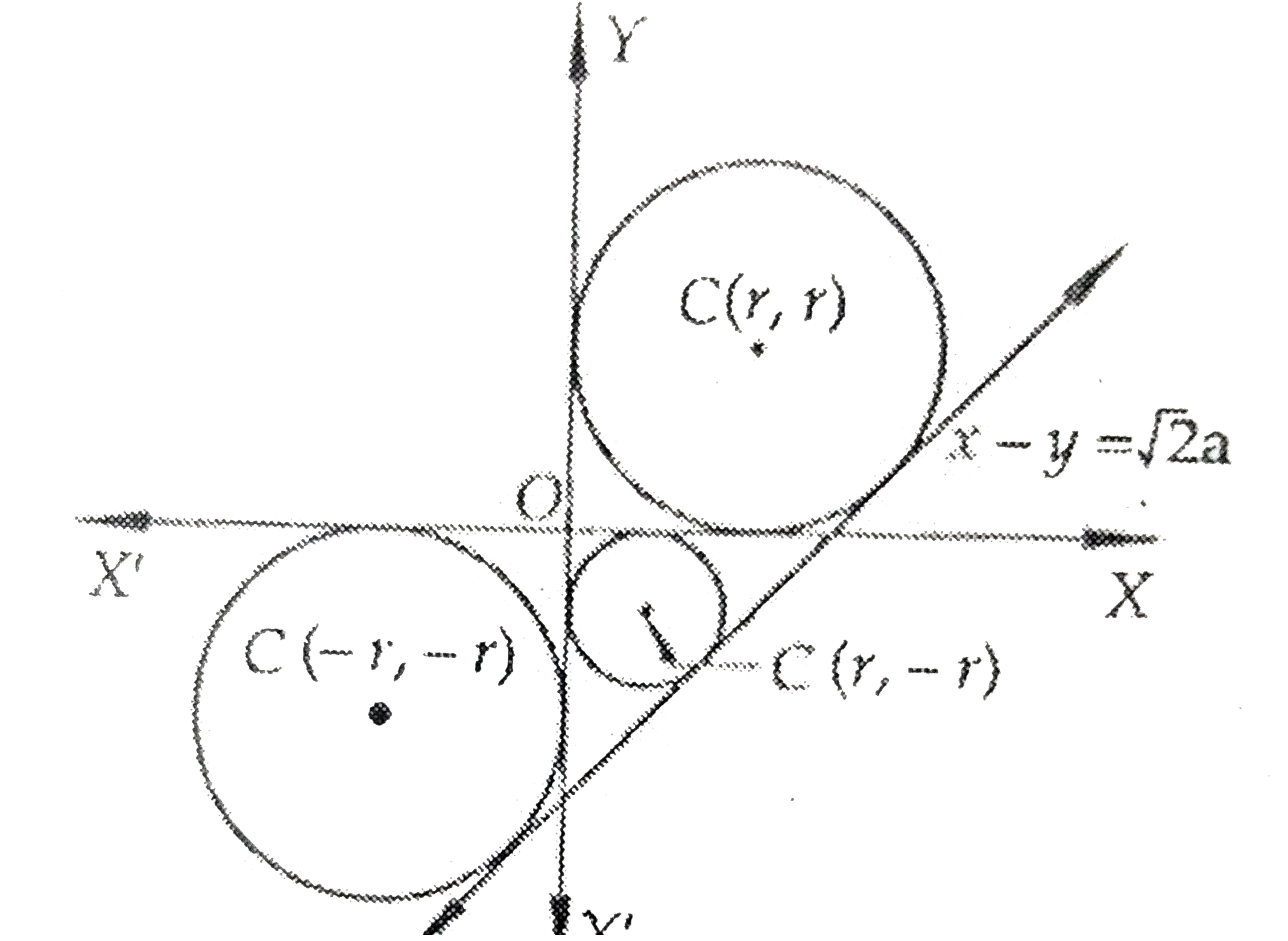
The circle touches x−y=√2a
∴∣∣∣−√2a√2∣∣∣=r when centre is at (r, r) or (-r, -r)
and ∣∣∣2r−√2a√2∣∣∣=r when centre is at (r, -r)
⇒r=aandr=(√2±1)a
|
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Video
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section II - Assertion Reason Type
12 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Chapter Test
55 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
31 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
59 Videos
Similar Questions
Knowledge Check
The circle that can be drawn to touch the coordinate axes and the line 4x+3y=12 cannot lie in
Afirst quadrantBsecond quadrantCthird quadrantDfourth quadrantFind the coordinates of the centre of the circle x2+y2−8x−4y=5.
A(2,4)B(−2,4)C(4,2)D(4,−2)A circle touches the x-axis and also touches the circle with centre (0,3) and radius 2. The locus of the centre of the circle is :
Aa circleBan ellipseCa parabolaDa hyperbola
A circle touching both the coordinates axes, having centre in the first quadrant and also touching the line
4x+3y=12 is given by
x2+y2−2cx−2xy+c2=0. Find the sum of all possible values of c.
View SolutionFind the equation of the circle which touches both the axes and the line x=c
View SolutionA circle touches the x-axis and also touches the circle with centre (0,3) and radius 2. The locus of the centre of the circle is
View SolutionNumber of circle touching both the axes and the line x+y=4 is greater than or equal to :
View SolutionA circle touches the line L and the circle C1 externally such that both the circles are on the same side of the line, then the locus of centre of the circle is :
View Solution
