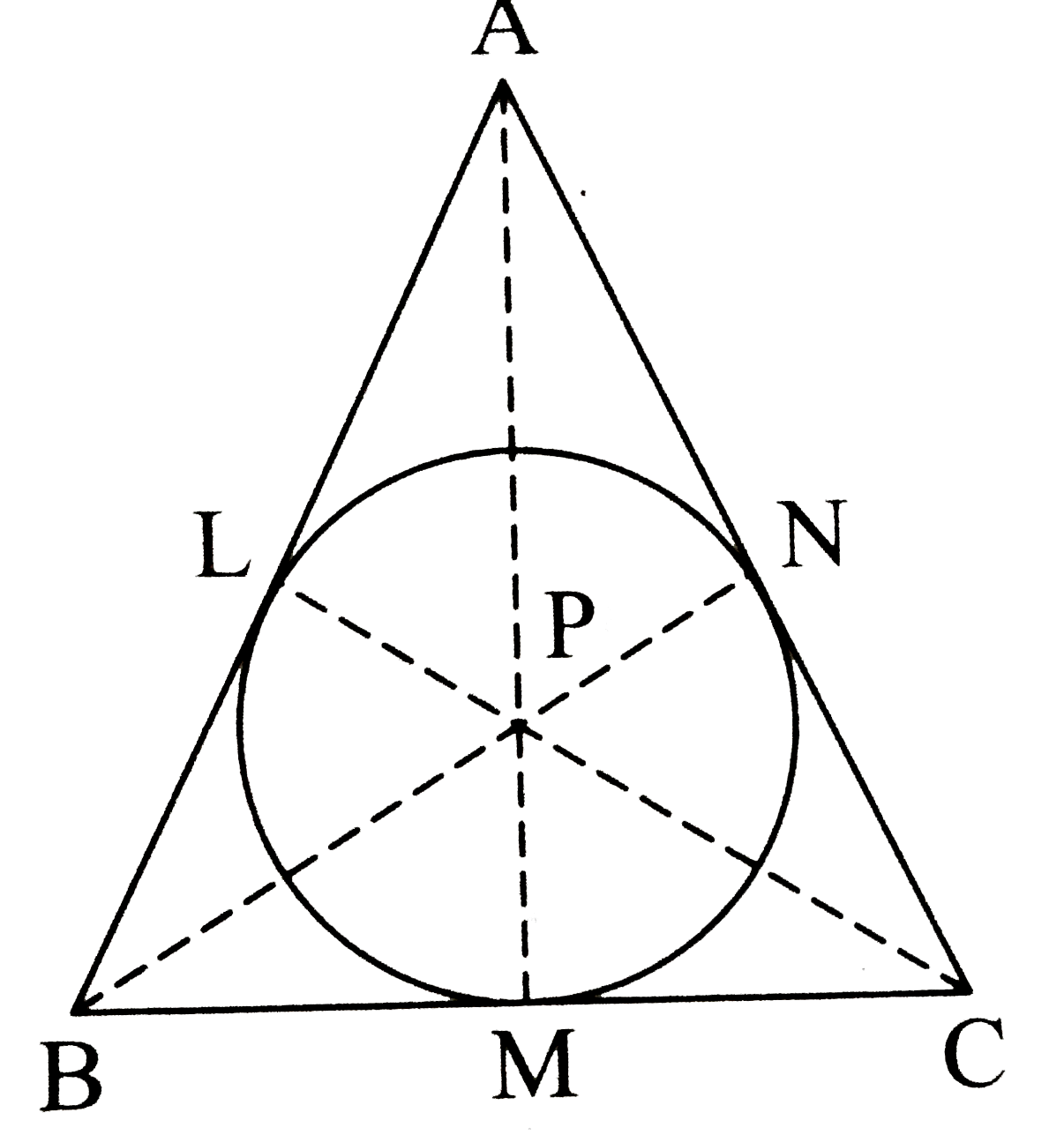
A circle with centre P is inscribed in the △ ABC. Side AB, side BC and side AC touch the circle at points L,M and N respectively. Radius of the circle is r. Prove that: A(△ABC)=12(AB+BC+AC)×r.
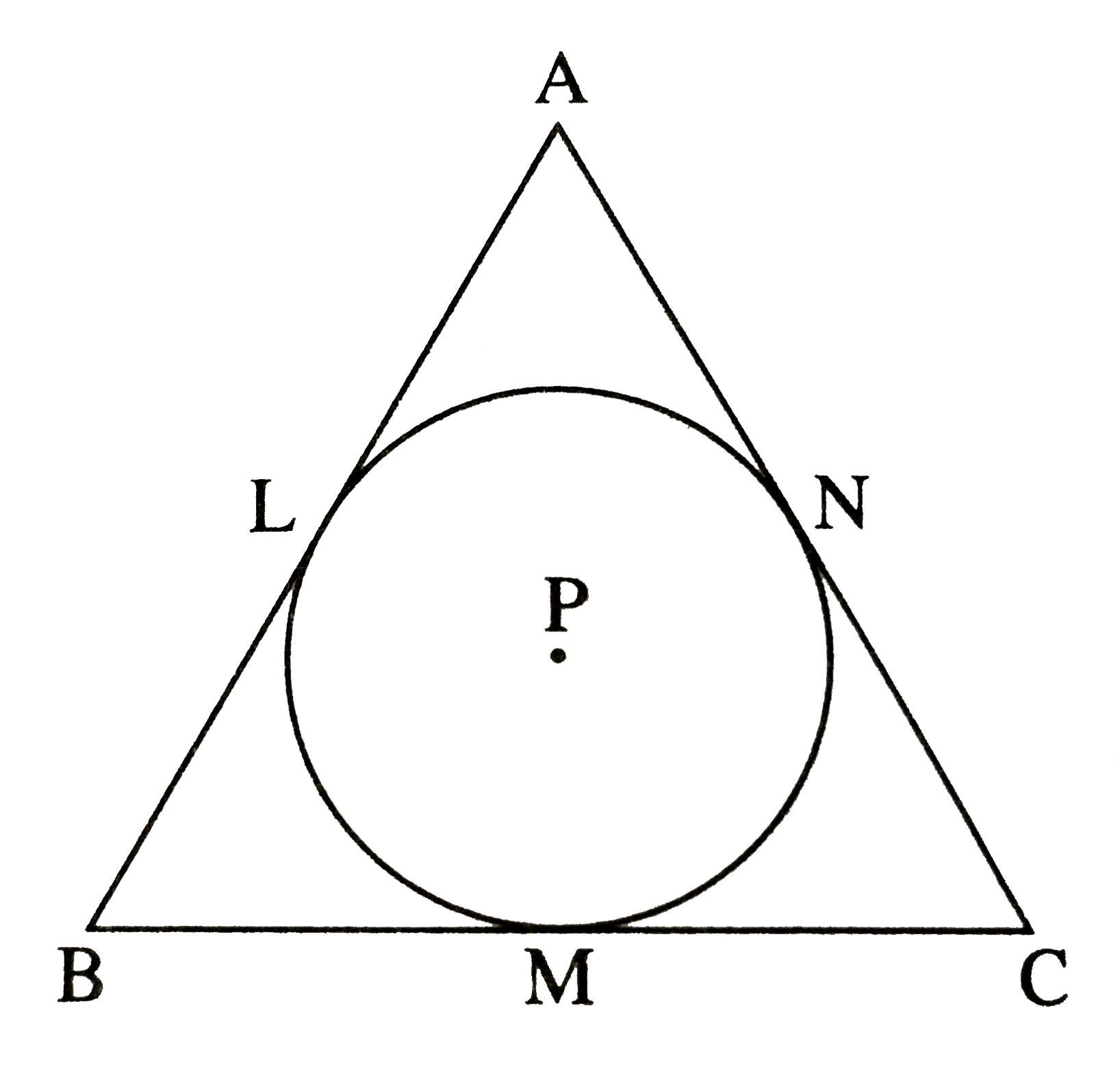
Step by step video & image solution for A circle with centre P is inscribed in the triangle ABC. Side AB, side BC and side AC touch the circle at points L,M and N respectively. Radius of the circle is r. Prove that: A( triangle ABC)=(1)/(2)(AB+BC+AC)xxr. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- BOARD QUESTION PAPER: MARCH 2019BOOK - TARGET PUBLICATIONCHAPTER - BOARD QUESTION PAPER: MARCH 2019EXERCISE - (Solve the following questions (Any three):
4 Videos
- ARITHMETIC PROGRESSION BOOK - TARGET PUBLICATIONCHAPTER - ARITHMETIC PROGRESSION EXERCISE - Chapter Assessment
17 Videos
- CHALLENGING QUESTIONS BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - Chapter 6: Statistics
4 Videos
Similar Questions
A circle with centre P is inscribed in the ΔABC Side AB, side BC and side A C touch the circle at points L,M and N respectively . Prove that :
A(ΔABC)=12(AB+BC+AC)×r
View SolutionA circle is inscribed in a triangle ABC. It touches the sides AB and AC at M and N respectively. If O is the centre of the circle and ∠A=70∘ , then what is ∠MON equal to ?
View Solution
Knowledge Check
A circle is inscribed in a triangle ABC. It touches the sides AB, BC and AC at the points R, P and Q respectively. If AQ = 4.5 cm, PC = 5.5 cm and BR = 6 cm, then the perimeter of the triangle ABC is:
एक वृत्त किसी त्रिभुज ABC में अन्तर्निहित है | यह भुजाओं AB, BC और AC को क्रमशः बिंदु R, P और Q पर स्पर्श करता है | यदि AQ = 4.5 सेमी, PC = 5.5 सेमी और BR = 6 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |A30.5cm.B28cm.C32cm.D26.5cm.ΔABC is an isosceles triangle and AB = AC. If all the sides AB. BC and CA of a ΔABC touch a circle at D, E and F respectively. Then BE is equal to :
A12 BCB13 BCC14 BCD23 BC
The side AB, BC and CA of triangle ABC touch a circle at P,Q and R respectively. If PA =4 cm, BP=3 cm and AC=11 cm, then length of BC is

View SolutionThe incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively . Prove that BD = DC.
View SolutionThe sides AB,BC and AC of a triangle ABC touch a circle with centre O and radius r at P, Q, and R respectively.
View SolutionThe incircle of an isosceles triangle ABC, with AB=AC, touches the sides AB, BC, CA at D,E and F respectively. Prove that E bisects BC.
View SolutionIn the given figure the sides AB, BE and CA of triangle ABC touch a circle with centre O and radius r at P,Q and R respectively.
Prove that : (i)AB+CQ=AC+BQ
(ii) Area (△ABC)=12(Perimeter of△ABC)×r

View SolutionIn triangle ABC,right angled at B, BC = 24 cm, and AB = 7 cm. A circle is inscribed in triangle ABC. Then the radius of the circle is:
View Solution
