A circle is inscribed in a triangle ABC. It touches the sides AB and AC at M and N respectively. If O is the centre of the circle and ∠A=70∘ , then what is ∠MON equal to ?
90∘
100∘
110∘
120∘
To solve the problem, we need to find the angle ∠MON in triangle ABC where a circle is inscribed. The circle touches the sides AB and AC at points M and N respectively, and the angle A is given as 70∘.
1. Understand the Geometry:
- We have triangle ABC with an inscribed circle.
- The points where the circle touches the sides are M on AB and N on AC.
- The center of the circle is denoted as O.
2. Identify Key Angles:
- Since M and N are points of tangency, the lines OM and ON are radii of the circle.
- The radius is perpendicular to the tangent line at the point of tangency. Therefore, we have:
∠AMO=90∘and∠ANO=90∘
3. Sum of Angles in Quadrilateral:
- The quadrilateral AMON consists of angles ∠AMO, ∠ANO, and ∠A.
- The sum of the angles in any quadrilateral is 360∘.
- Thus, we can write:
∠AMO+∠ANO+∠A+∠MON=360∘
4. Substituting Known Values:
- We know:
∠AMO=90∘,∠ANO=90∘,and∠A=70∘
- Substituting these values into the equation gives:
90∘+90∘+70∘+∠MON=360∘
- Simplifying this:
250∘+∠MON=360∘
5. Solving for ∠MON:
- To find ∠MON, we rearrange the equation:
∠MON=360∘−250∘=110∘
Final Answer:
Thus, ∠MON=110∘.
- We have triangle ABC with an inscribed circle.
- The points where the circle touches the sides are M on AB and N on AC.
- The center of the circle is denoted as O.
- Since M and N are points of tangency, the lines OM and ON are radii of the circle.
- The radius is perpendicular to the tangent line at the point of tangency. Therefore, we have:
∠AMO=90∘and∠ANO=90∘
- The quadrilateral AMON consists of angles ∠AMO, ∠ANO, and ∠A.
- The sum of the angles in any quadrilateral is 360∘.
- Thus, we can write:
∠AMO+∠ANO+∠A+∠MON=360∘
- We know:
∠AMO=90∘,∠ANO=90∘,and∠A=70∘
- Substituting these values into the equation gives:
90∘+90∘+70∘+∠MON=360∘
- Simplifying this:
250∘+∠MON=360∘
- To find ∠MON, we rearrange the equation:
∠MON=360∘−250∘=110∘
Thus, ∠MON=110∘.
Similar Questions
In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F respectively. If AB= 12 cm, BC= 8 cm and AC = 10 cm, find the lengths of AD, BE and CF.
View SolutionA circle touches the side BC of ΔABC at F and touches AB and AC at D and E, respectively. If AD = 8 cm, then find the perimeter of ΔABC.

View Solution
Knowledge Check
A circle is inscribed in a triangle ABC. It touches the sides AB, BC and AC at the points R, P and Q respectively. If AQ = 4.5 cm, PC = 5.5 cm and BR = 6 cm, then the perimeter of the triangle ABC is:
एक वृत्त किसी त्रिभुज ABC में अन्तर्निहित है | यह भुजाओं AB, BC और AC को क्रमशः बिंदु R, P और Q पर स्पर्श करता है | यदि AQ = 4.5 सेमी, PC = 5.5 सेमी और BR = 6 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |A30.5cm.B28cm.C32cm.D26.5cm.In the given figure, AB and AC are tangents to the circle at B and C respectively and O is the centre of the circle, then x equals
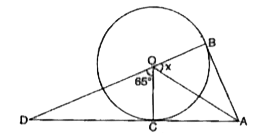 A65∘B32.5∘C57.5∘D45∘
A65∘B32.5∘C57.5∘D45∘The in circle of ΔABC touches the sides BC, CA and AB at D, E and F respectively. Then AF + BD + CE is equal to :
A12 (Perimeter of Δ ABC)B13 (Perimeter of Δ ABC)C14 (Perimeter of Δ ABC)DPerimeter of Δ ABC
ABC is an isosceles triangle and AC, BC are the tangent at M and N respectively. DE is the diameter of the circle. ∠ADP=∠BEQ=100∘. What is the value of ∠PRD?
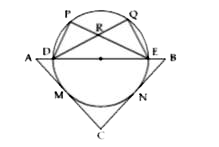
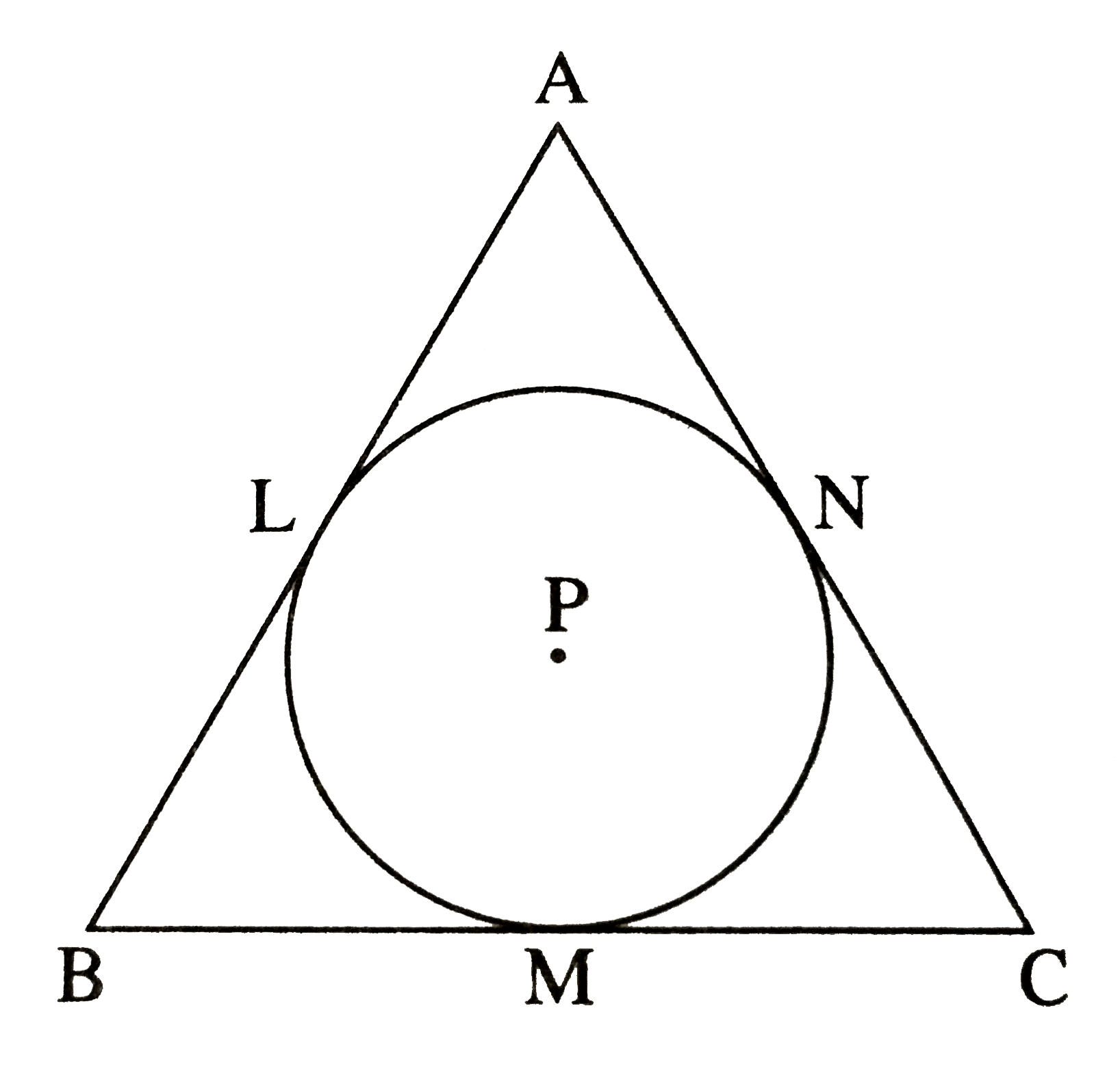
View SolutionA circle with centre P is inscribed in the △ ABC. Side AB, side BC and side AC touch the circle at points L,M and N respectively. Radius of the circle is r. Prove that: A(△ABC)=12(AB+BC+AC)×r.
View SolutionThe circle inscribed in the triangle ABC touches the side BC, CA and AB in the point A1B1andC1 respectively. Similarly the circle inscribed in the ΔA1B1C1 touches the sieds in A2,B2,C2 respectively and so on. If AnBnCn be the nth Δ so formed, prove that its angle are
(C−π3). Hence prove that the triangle so formed is ultimately equilateral.
View SolutionVarun has been selected by his School to design logo for Sports Day T-shirts for students and staff . The logo design is as given in the figure and he is working on the

fonts and different colours according to the theme. In given figure, a circle with centre O is inscribed in a ΔABC, such that it touches the sides AB, BC and CA at points D, E and F respectively. The lengths of sides AB, BC and CA are 12 cm, 8 cm and 10 cm respectively.

if radius of the circle is 4 cm , Find the area of ΔAOB.
View SolutionA circle is inscribed in a equilateral triangle of side 24 cm. What is the area ( in cm2 ) of a square inscribed in the circle ?
View Solution
