A company manufactures two types of toys A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. He earns a profit of Rs.50 each on type A and Rs.60 each on type. B. How many toys of each type should the company manufacture in a day to maximize the profit ?
The correct Answer is:12 toys of type A and 15 toys of type B to earn maximum profit Rs. 1500
To solve the problem of maximizing the profit from manufacturing two types of toys (A and B), we will follow these steps:
Step 1: Define Variables
Let:
- X = number of Type A toys produced
- Y = number of Type B toys produced
Step 2: Formulate the Objective Function
The profit from each type of toy is given as:
- Profit from Type A = Rs. 50 per toy
- Profit from Type B = Rs. 60 per toy
Thus, the total profit Z can be expressed as:
Z=50X+60Y
We want to maximize Z.
Step 3: Set Up the Constraints
From the problem, we have the following constraints based on the cutting and assembling times:
1. Cutting Time Constraint:
- Type A requires 5 minutes for cutting.
- Type B requires 8 minutes for cutting.
- Total available cutting time = 3 hours = 180 minutes.
Therefore, the cutting time constraint can be written as:
5X+8Y≤180
2. Assembling Time Constraint:
- Type A requires 10 minutes for assembling.
- Type B requires 8 minutes for assembling.
- Total available assembling time = 4 hours = 240 minutes.
Therefore, the assembling time constraint can be written as:
10X+8Y≤240
3. Non-negativity Constraints:
X≥0,Y≥0
Step 4: Solve the Constraints
We will solve the inequalities to find the feasible region.
1. Cutting Time Constraint:
5X+8Y=180
- If X=0:
8Y=180⇒Y=22.5
- If Y=0:
5X=180⇒X=36
So, the line intersects the axes at points (0,22.5) and (36,0).
2. Assembling Time Constraint:
10X+8Y=240
- If X=0:
8Y=240⇒Y=30
- If Y=0:
10X=240⇒X=24
So, the line intersects the axes at points (0,30) and (24,0).
Step 5: Graph the Constraints
Plot the lines on a graph to identify the feasible region. The feasible region is bounded by the lines and the axes.
Step 6: Identify Corner Points
The corner points of the feasible region can be found by solving the equations of the lines:
1. Intersection of 5X+8Y=180 and 10X+8Y=240:
5X+8Y=180(1)
10X+8Y=240(2)
Subtract (1) from (2):
5X=60⇒X=12
Substitute X=12 into (1):
5(12)+8Y=180⇒60+8Y=180⇒8Y=120⇒Y=15
So, one corner point is (12,15).
2. Other corner points are (0,30), (24,0), and (0,22.5).
Step 7: Evaluate the Objective Function at Each Corner Point
1. At (0,30):
Z=50(0)+60(30)=1800
2. At (24,0):
Z=50(24)+60(0)=1200
3. At (12,15):
Z=50(12)+60(15)=600+900=1500
4. At (0,22.5):
Z=50(0)+60(22.5)=1350
Step 8: Determine the Maximum Profit
The maximum profit occurs at the point (0,30) with a profit of Rs. 1800.
Conclusion
To maximize profit, the company should produce:
- 0 Type A toys
- 30 Type B toys
Let:
- X = number of Type A toys produced
- Y = number of Type B toys produced
The profit from each type of toy is given as:
- Profit from Type A = Rs. 50 per toy
- Profit from Type B = Rs. 60 per toy
Z=50X+60Y
We want to maximize Z.
From the problem, we have the following constraints based on the cutting and assembling times:
- Type A requires 5 minutes for cutting.
- Type B requires 8 minutes for cutting.
- Total available cutting time = 3 hours = 180 minutes.
5X+8Y≤180
- Type A requires 10 minutes for assembling.
- Type B requires 8 minutes for assembling.
- Total available assembling time = 4 hours = 240 minutes.
10X+8Y≤240
X≥0,Y≥0
We will solve the inequalities to find the feasible region.
5X+8Y=180
- If X=0:
8Y=180⇒Y=22.5
- If Y=0:
5X=180⇒X=36
10X+8Y=240
- If X=0:
8Y=240⇒Y=30
- If Y=0:
10X=240⇒X=24
Plot the lines on a graph to identify the feasible region. The feasible region is bounded by the lines and the axes.
The corner points of the feasible region can be found by solving the equations of the lines:
1. Intersection of 5X+8Y=180 and 10X+8Y=240:
5X+8Y=180(1)
10X+8Y=240(2)
Subtract (1) from (2):
5X=60⇒X=12
Substitute X=12 into (1):
5(12)+8Y=180⇒60+8Y=180⇒8Y=120⇒Y=15
So, one corner point is (12,15).
1. At (0,30):
Z=50(0)+60(30)=1800
2. At (24,0):
Z=50(24)+60(0)=1200
3. At (12,15):
Z=50(12)+60(15)=600+900=1500
4. At (0,22.5):
Z=50(0)+60(22.5)=1350
The maximum profit occurs at the point (0,30) with a profit of Rs. 1800.
To maximize profit, the company should produce:
- 0 Type A toys
- 30 Type B toys
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - RS AGGARWALCHAPTER - LINEAR PROGRAMMINGEXERCISE - EXPRCISE 33B (LONG-ANSWER QUESTIONS)
3 Videos
- LINEAR PROGRAMMINGBOOK - RS AGGARWALCHAPTER - LINEAR PROGRAMMINGEXERCISE - SECTION A
4 Videos
- LINEAR PROGRAMMINGBOOK - RS AGGARWALCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exprcise 33A
11 Videos
- LINEAR DIFFERENTIAL EQUATIONS BOOK - RS AGGARWALCHAPTER - LINEAR DIFFERENTIAL EQUATIONS EXERCISE - Objective Questions
27 Videos
- MATRICESBOOK - RS AGGARWALCHAPTER - MATRICESEXERCISE - Exercise 5F
21 Videos
Similar Questions
A copany manufactures two types of toys, A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. The profit is Rs.50 each on type A and Rs.60 each on type B. How many toys of each type should the company manufacture in a day to maximize the profit?
View SolutionA company manufacturers two types of products P and Q. The product P requires 5 minutes each for cutting and 10 minutes each for assembling. The product Q requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes availabe for cutting and 4 hours for assembling. The profit is 50 paise each for type P and 60 paise each for type Q. How many products of each type should the company manufacture in order to maximize the profit?
View SolutionA company manufacturers two types of novelty suouvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours for assembling. The profit is Rs. 5 each for type A and Rs. 6 each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximise the profit?
View SolutionA company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours for assembling. The profit is Rs 5 each for type A and Rs 6 each for type B souvenirs. How many souvenirs of each type should the company manufacture m order to maximise the profit?
View SolutionA factory makes two types of items A and B, made of plywood. One piece of item A requires 5 minutes for cutting and 10 minutes for assembling. One piece of item B requires 8 minutes for cutting and 8 minutes for assembling. There are 3 hours and 20 minutes available for cutting and 4 hours for assembling. The profit on one piece of item A is Rs 5 and that on item B is Rs 6. How many pieces of each type should the factory make so as to maximise profit? Make it as an L.P.P. and solve it graphically.
View SolutionA company manufactures two type of novelty souvenirs made of plywood, Souvenirs of type A recquire 8 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 10 minutes each for cutting and 15 minutes each for assembling. There are 4 hours available for for assembling. THere are 4 hours available for cutting and 5 hours available for assembling. The profit is 60 paise on each itme of type A and 75 paise on each item of tyep B. Formulate the above information as a linear programming problem.
View SolutionA manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each purpose and the time (in minutes) required for each toy on the machines is given below:
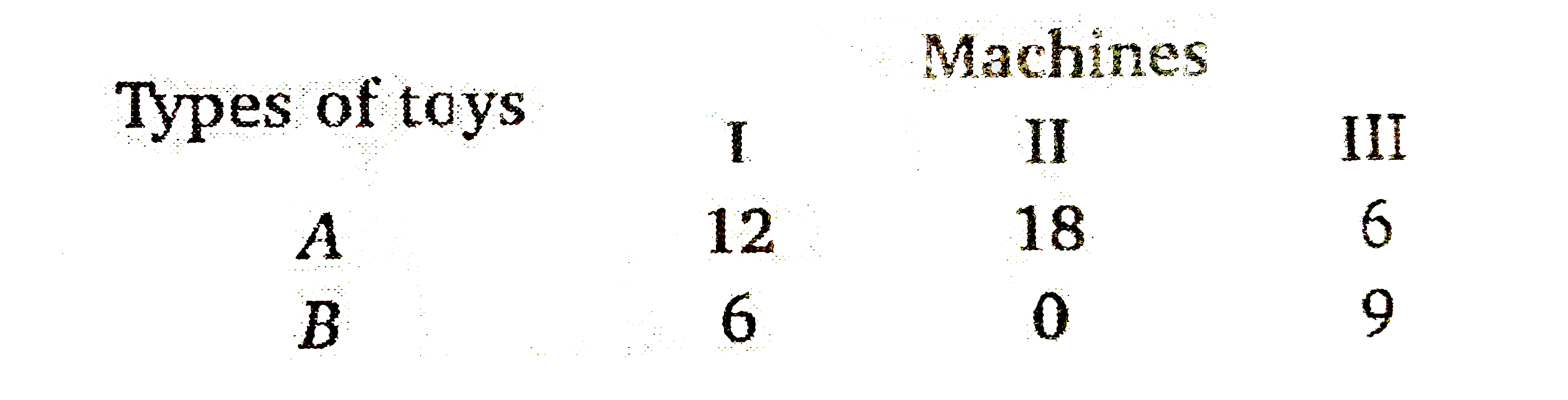
Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs. 7.50 and that on each toy of type B is Rs. 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
View SolutionA manufacturing company makes two types of teaching aids A and B . Each type of A requires 9 labour hours for fabricating and 1 labour hours for finishing.Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing.For fabricating and finishing, the maximum labour hours abailable per week are 180 and 30 respectively.The company makes a profit of ₹ 80 on each type A and ₹ 120 on each type B. How many pieces of type A and type B should be manufactured per week to get a maximum profit? Make it as an LPP and solve graphically.What is the maximum profit per week?
View SolutionIn a small scale industry, a manufacturer produces two types of book cases. The first type of book case requires 3 hours on machine A and 2 hours on machine B for completion whereas the second type of book case requires 3 hours on machine A and 3 hours on machine B. The machines A and B respectively run for at the most 18 hours and 14 hours per day. He earns a profit of 30 on each type of case of first type and 40 on each book case of second type. How many book cases of each type should he manufacture so as to have maximum profit. Make it an LPP and solve it graphically.
View SolutionA manufacturing company makes two types of teaching aids A and B . Each type of A requires 9 labour hours for fabricating and 1 labour hours for finishing.Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing.For fabricating and finishing, the maximum labour hours abailable per week are 180 and 30 respectively.The company makes a profit of ₹ 80 on each type A and ₹ 120 on each type B. How many pieces of type A and type B should be manufactured per week to get a maximum profit? Make it as an LPP and solve graphically.What is the maximum profit per week?
View Solution
