A discrete random variable X has the probability distribution as given below
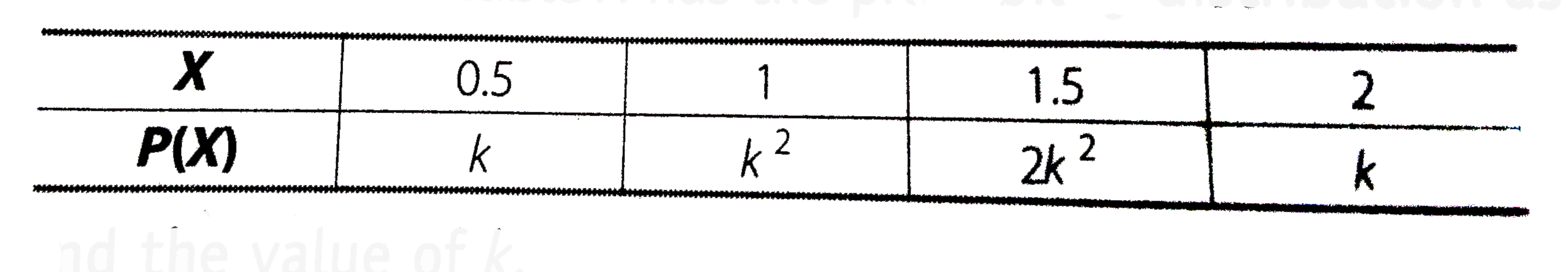
(i) Find the value of k.
(ii) Determine the mean of the distribution.
Video Solution
Text Solution
We have,

(i) We know that, n∑i=1Pi=1, where Pi≥0
⇒P1+P2+P3+P4=1
⇒k+k2+2k2+k=1
⇒3k2+2k−1=0
⇒3k2+3k−k−1=0
⇒(3k−1)(k+1)=0
⇒k=1/3⇒k=−1
Since, k is ≥0⇒k=1/3
(ii) Mean of the distribution (μ)=E(X)=n∑i=1ixiPi
=0.5(k)+1(k2+1.5(2k2)+2(k)=4k2+2.5k
=4⋅19+2.5⋅13
=4+7.59=2318
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
A random variable X has the probability distribution given below
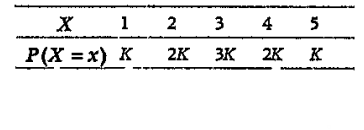
Its variance isA163B43C53D103A random variable has the following probability distribution

The value of p isA110B-1C310DNone of these
A random variable X has the follwing probability distribution:

Find k.
View SolutionA random variable X has the following probability distribution find K.

View SolutionA random variable X has the following probability distribution:

Then E(X) = …….
View SolutionA random variable has the following probability distribution
The value of p is

View SolutionThe random variable X has the following probability distribution
Then, F(0) is equal to

View SolutionA random variable X has the follwing probability distribution:

Find P(0<X<4)
View Solution

