A function is said to be even if f(x)=f(-x). Which of the following is not an even function?
y=|x|
y=secx
y=logx2
y=x2+sinx
The correct Answer is:D
To determine which of the given functions is not an even function, we need to check if each function satisfies the condition f(x)=f(−x).
1. Understanding Even Functions:
A function f(x) is considered even if for every x, f(x)=f(−x). This means the function's graph is symmetric about the y-axis.
2. Analyzing Each Function:
- Function 1: f(x)=|x|
To check if it's even:
f(−x)=|−x|=|x|=f(x)
This function is even.
- Function 2: f(x)=secx
To check if it's even:
f(−x)=sec(−x)=1cos(−x)=1cosx=secx=f(x)
This function is even.
- Function 3: f(x)=log(x2)
To check if it's even:
f(−x)=log((−x)2)=log(x2)=f(x)
This function is even.
- Function 4: f(x)=x2+sinx
To check if it's even:
f(−x)=(−x)2+sin(−x)=x2−sinx
Since sin(−x)=−sinx, we have:
f(−x)=x2−sinx≠f(x)=x2+sinx
This function is not even.
3. Conclusion:
The function that is not even is f(x)=x2+sinx.
Final Answer:
The function that is not an even function is f(x)=x2+sinx.
---
A function f(x) is considered even if for every x, f(x)=f(−x). This means the function's graph is symmetric about the y-axis.
- Function 1: f(x)=|x|
To check if it's even:
f(−x)=|−x|=|x|=f(x)
This function is even.
To check if it's even:
f(−x)=sec(−x)=1cos(−x)=1cosx=secx=f(x)
This function is even.
To check if it's even:
f(−x)=log((−x)2)=log(x2)=f(x)
This function is even.
To check if it's even:
f(−x)=(−x)2+sin(−x)=x2−sinx
Since sin(−x)=−sinx, we have:
f(−x)=x2−sinx≠f(x)=x2+sinx
This function is not even.
The function that is not even is f(x)=x2+sinx.
The function that is not an even function is f(x)=x2+sinx.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A function f(x) is defined as even if and only if f(x)=f(−x) for all real values of x. Which one of the following graphs represents an even function f(x) ?
A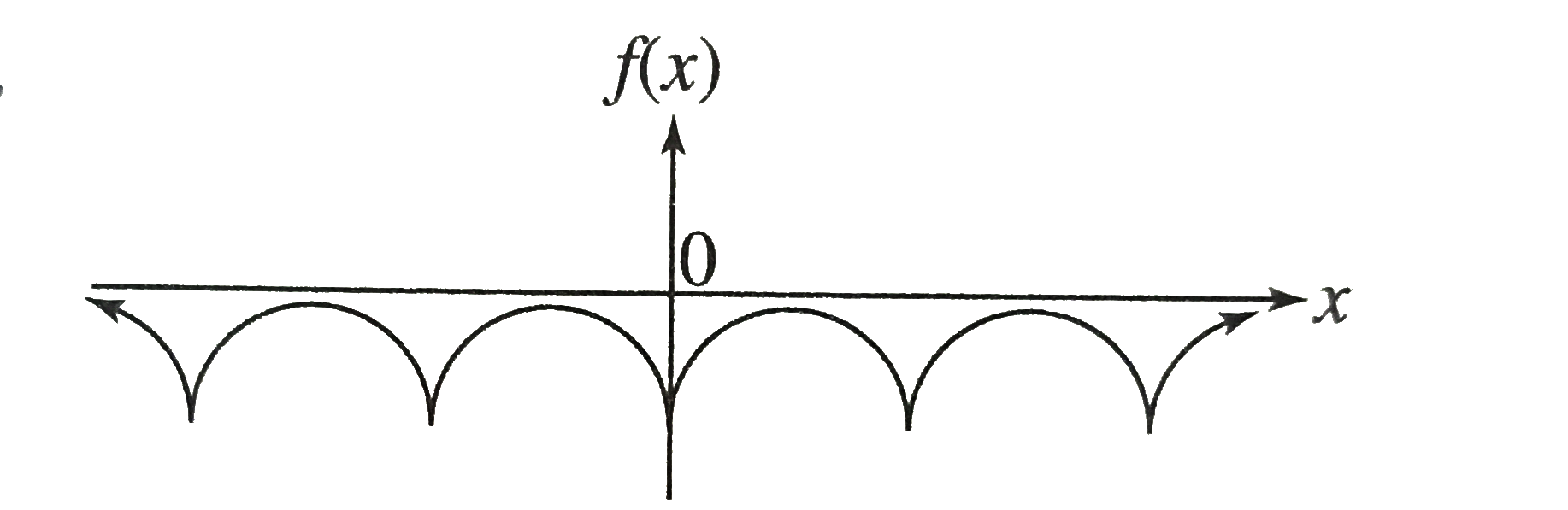 B
B C
C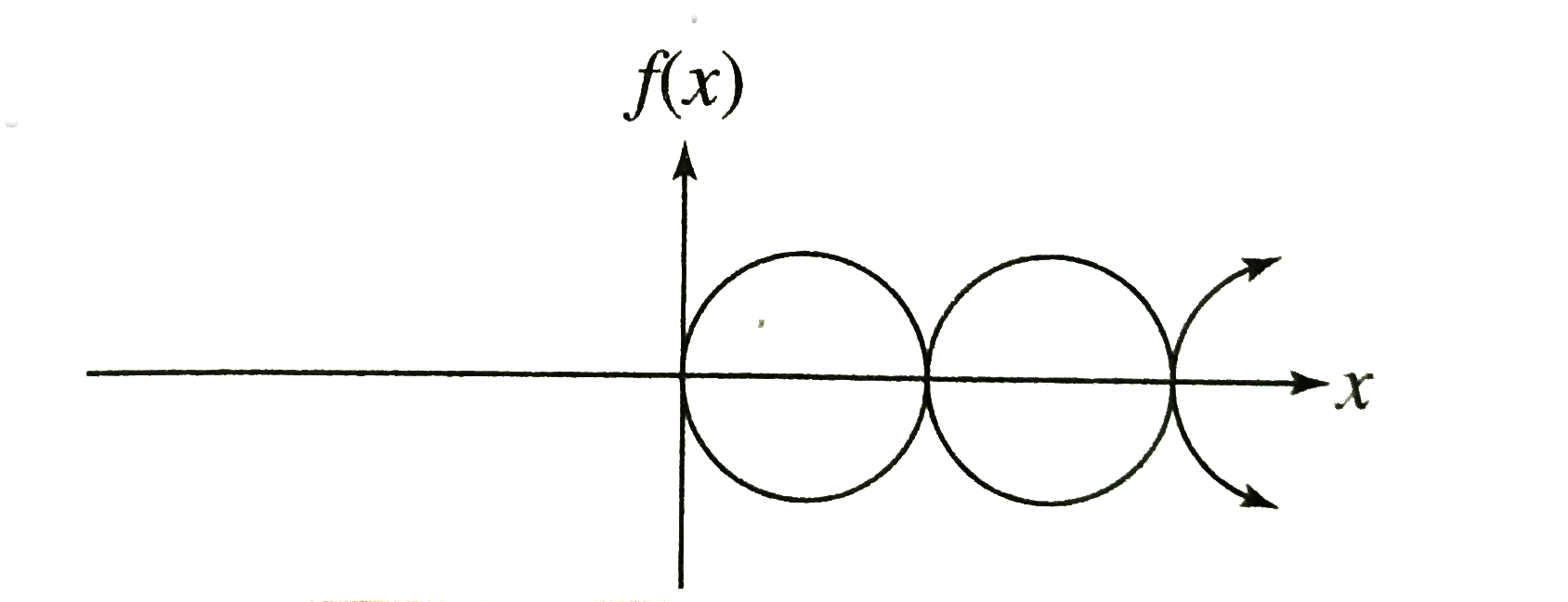 D
D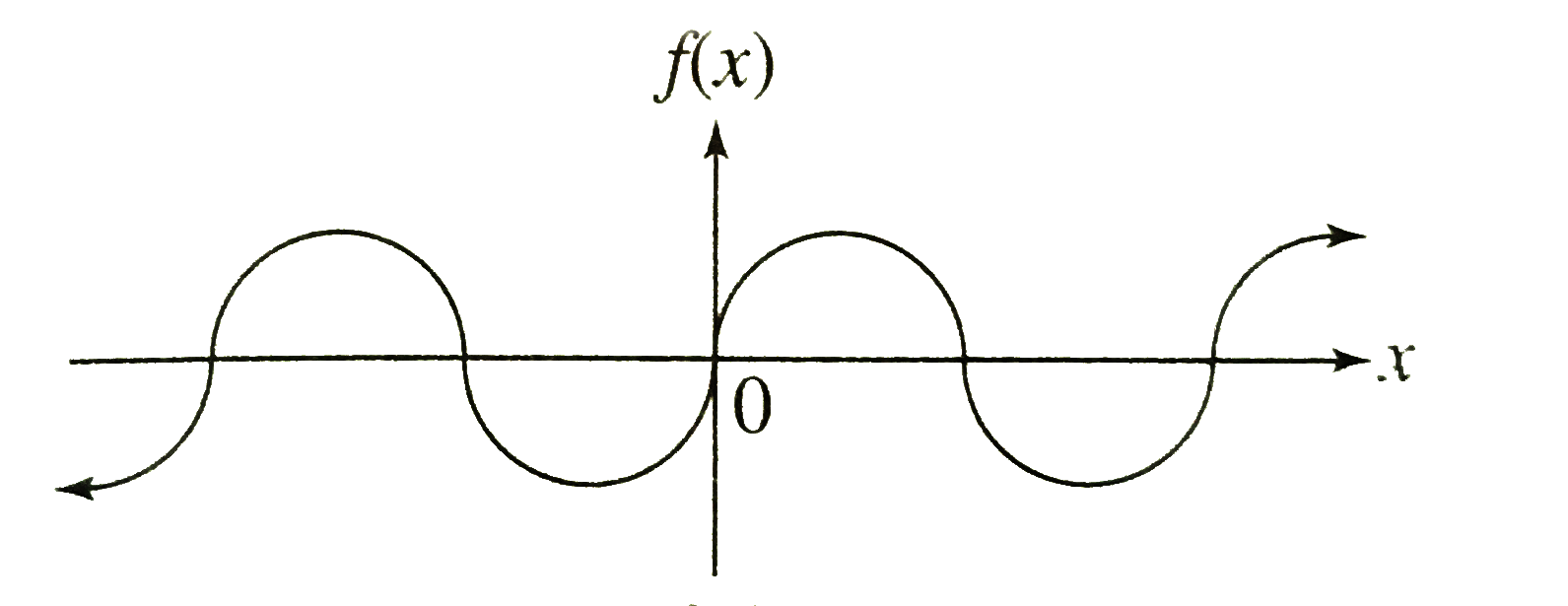
For which of the following functions does f(x)f(2−x) ?
Af(x)=x+2Bf(x)=2x−x2Cf(x)=2−xDf(x)=(2−x)2
The graph of the function y=f(x). Then which of the following curve represent the graph of the function y=|f(x)|
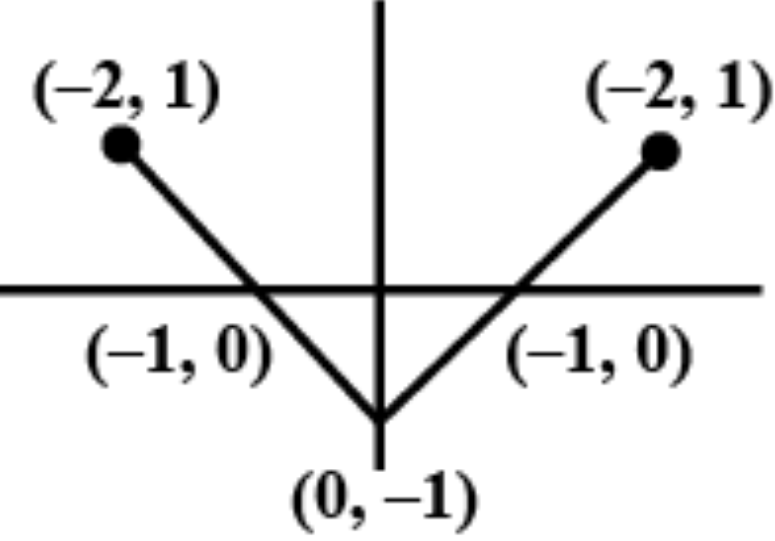
View SolutionShow that ax+a−x is an even function.
View SolutionGiven a function, f(x), such that f(x) = f(|x|). Which one of the following could be the graph of f(x) ?
View SolutionLeft hand derivative and right hand derivative of a function f(x) at a point x=a are defined as
f'(a−)=limh→0+f(a)−f(a−h)h
=limh→0+f(a+h)−f(a)h
andf'(a+)=limh→0+f(a+h)−f(a)h
=limh→0+f(a)−f(a+h)h
=limh→0+f(a)−f(x)a−x respectively.
Let f be a twice differentiable function. We also know that derivative of a even function is odd function and derivative of an odd function is even function.
If f is even function, which of the following is right hand derivative of f' at x=a?
View SolutionLet f:(−π2,π2)→R be given by f(x)=(log(secx+tanx))3 then f(x) is an odd function f(x) is a one-one function f(x) is an onto function f(x) is an even function
View SolutionFor the function f(x)=ex1+ex, which of the following hold good? f is monotonic in its entire domain. Maximum of f is not attained even though f is bounded f has a point of inflection. f has one asymptote.
View Solution
