A graphic designer created an image for a school banner. He uses this image for small and medium banners. To produce a large banner, the designed increase the size of the image by 12.5% to 18 inches tall by 22.5 inches wide. What was the size of the original image?
15 inches by 17.5 inches
15 inches by 18 inches
16 inches by 18.5 inches
16 inches by 20 inches
The correct Answer is:D
To find the size of the original image before the designer increased its dimensions by 12.5%, we can follow these steps:
Step 1: Understand the increase in dimensions
The designer increased the dimensions of the image by 12.5%. This means the new dimensions (after the increase) represent 112.5% of the original dimensions.
Step 2: Set up the equations
Let the original height of the image be H inches and the original width be W inches. After the increase, the height and width are given as:
- Height = 18 inches
- Width = 22.5 inches
We can express this mathematically as:
- 112.5% of H=18
- 112.5% of W=22.5
Step 3: Convert percentages to decimal
To convert 112.5% to a decimal, we divide by 100:
112.5%=112.5100=1.125
Step 4: Solve for the original height
Using the equation for height:
1.125H=18
To find H, divide both sides by 1.125:
H=181.125
Calculating this gives:
H=16 inches
Step 5: Solve for the original width
Using the equation for width:
1.125W=22.5
To find W, divide both sides by 1.125:
W=22.51.125
Calculating this gives:
W=20 inches
Step 6: Conclusion
The original dimensions of the image were:
- Height = 16 inches
- Width = 20 inches
Thus, the size of the original image is 16 inches tall by 20 inches wide.
---
The designer increased the dimensions of the image by 12.5%. This means the new dimensions (after the increase) represent 112.5% of the original dimensions.
Let the original height of the image be H inches and the original width be W inches. After the increase, the height and width are given as:
- Height = 18 inches
- Width = 22.5 inches
- 112.5% of H=18
- 112.5% of W=22.5
To convert 112.5% to a decimal, we divide by 100:
112.5%=112.5100=1.125
Using the equation for height:
1.125H=18
To find H, divide both sides by 1.125:
H=181.125
H=16 inches
Using the equation for width:
1.125W=22.5
To find W, divide both sides by 1.125:
W=22.51.125
W=20 inches
The original dimensions of the image were:
- Height = 16 inches
- Width = 20 inches
Topper's Solved these Questions
Similar Questions
A student focuses the image of a well illuminated distant object on a screen using a convex lens. After that the gradually moves the object towards the lens and each time focuses its image on the screen by adjucting the lens.
(a) In which direction -towards the screen or away from the screen, does he move the lens ?
(b)What happens to the size of the image-does it decrease or increase ?
(c) What happens to the image on the screen when he moves the object very close to the lens ?View SolutionA student focuses the image of a candle flame, placed at about 2 m from a convex lens of focal length 10 cm, on a screen. After that, he moves gradually the flame towards the lens and each time its image on the screen.
(a) In which direction does he move the lens to focus the flame on the screen?
(b) What happens to the size of the image of the flame formed on the screen ?
(c ) What difference is seen in the intensity (brightnees) of the image of the flame on the screen ?
(d) What is seen on the when the flame is very close (at about 5 cm) to the lens ?View SolutionAn object 5 cm tall is placed 1 m from a concave spherical mirror which has a radius of curvature of 20 cm. The size of the image is
View SolutionAn object 5 cm tall is placed 1 m from a concave spherical mirror which has a radius of curvature of 20 cm. The size of the image is
View SolutionAn object of size 2cm is placed at a distance of 40cm from a glass lens, close to the principal axis of the lens, and the lens forms an image of size 2cm. What is the size of the image and what type of image is formed if the lens and the object, in the same arrangement, is immersed into water ? The refractive index of the lens 1.5, and that of the water is 1.33.
View SolutionA student focussed the flame of a candle on a screen with the help of a convex lens. He noted the positions of candle, lens and screen on the scale as given below:
Position of candle = 14.0 cm, Position of convex lens = 50.0 cm, Position of screen = 86.0 cm
(i) Find the focal length of the lens.
(ii) If under the given condition, height of the flame is 1.5 cm, what would be the height of image obtained on the screen?
(iii) If he displaces the candle to 32.0 cm, where will the image be formed and what will be its nature? Give reason for your answer.
(iv) After this if he further displaces the candle towards the lens, what will be the nature of the image formed and where will it be?
(v) Draw a ray diagram to show the formation of image in the above mentioned case.
[Hints. (i) u = (50-14) cm = 36 cm, v = (86 - 50) cm = 36 cm.
Thus the object is at 2f. Therefore f = 18cm
(ii) Height will be same, i.e., 1.5 cm
(iii) u = 50-32 = 18 cm. Thus, object will be at focus. Therefore, image will be at infinity and is real, inverted and enlarged.
(iv) Object will come in between focus and optical centre.
Image will be virtual, erect and enlarged and formed on the same side of lens as the object.View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
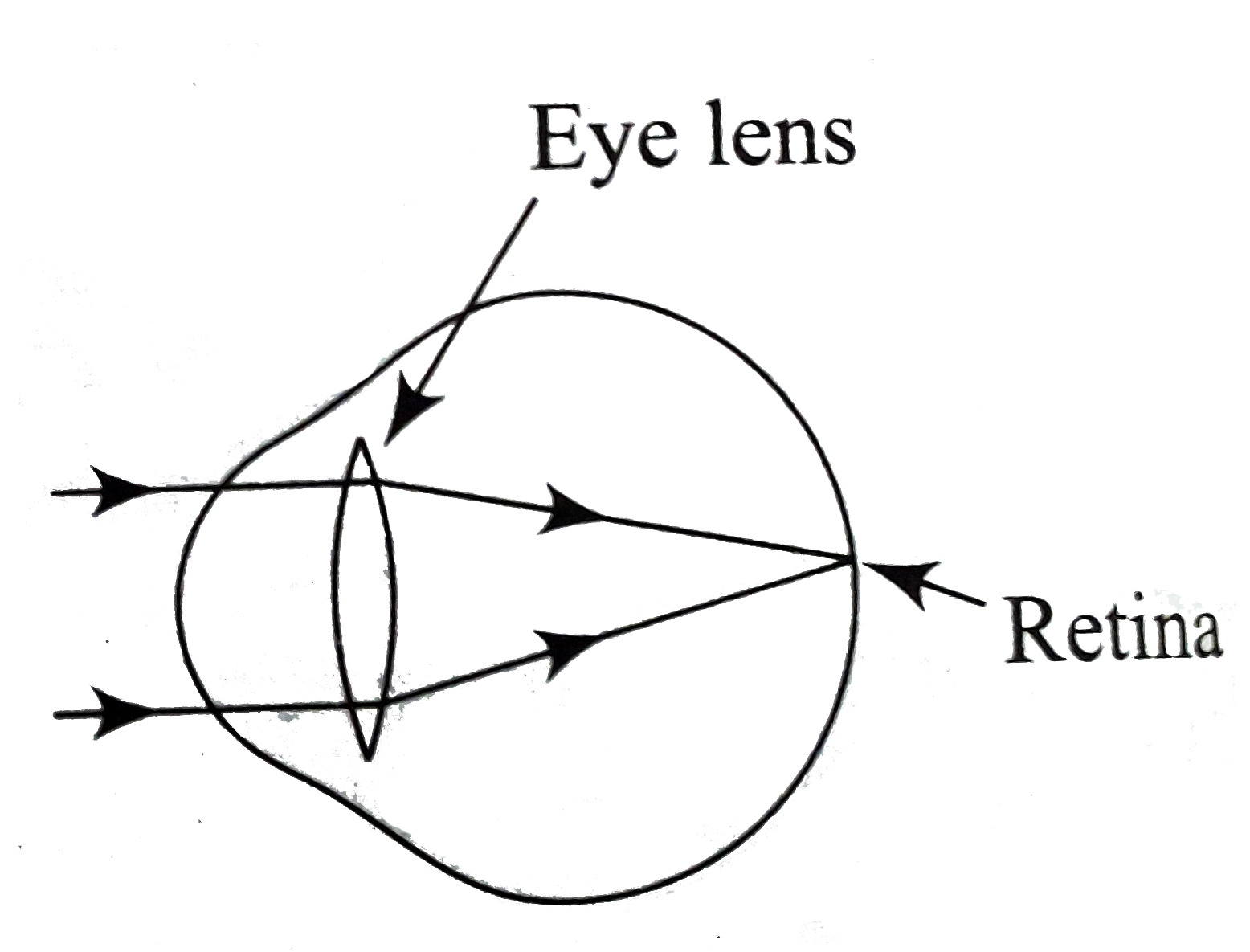
Q. Minimum focal length of eye lens of a normal peson isView SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
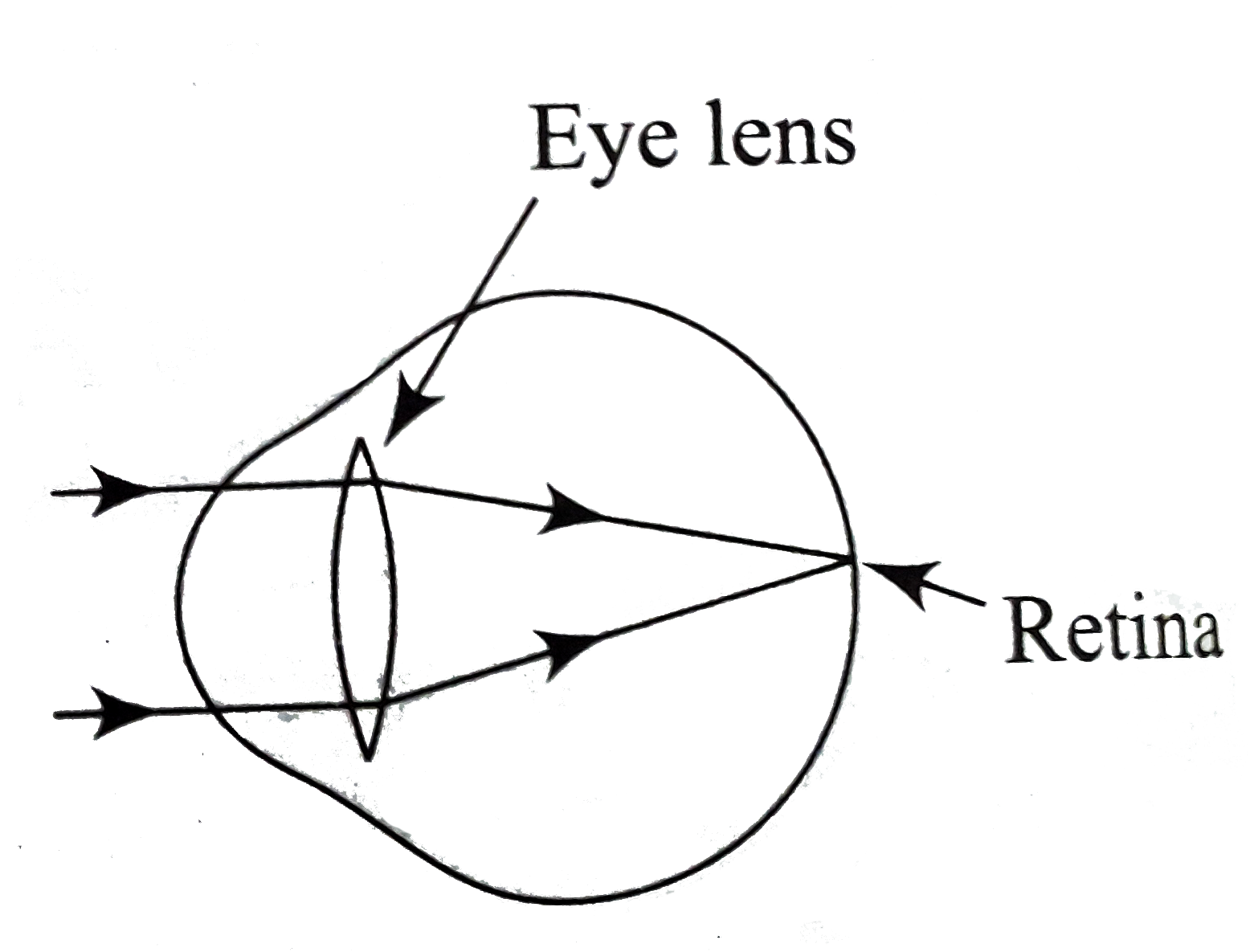
Q. Maximum focal length of a eye lens of a normal person isView SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
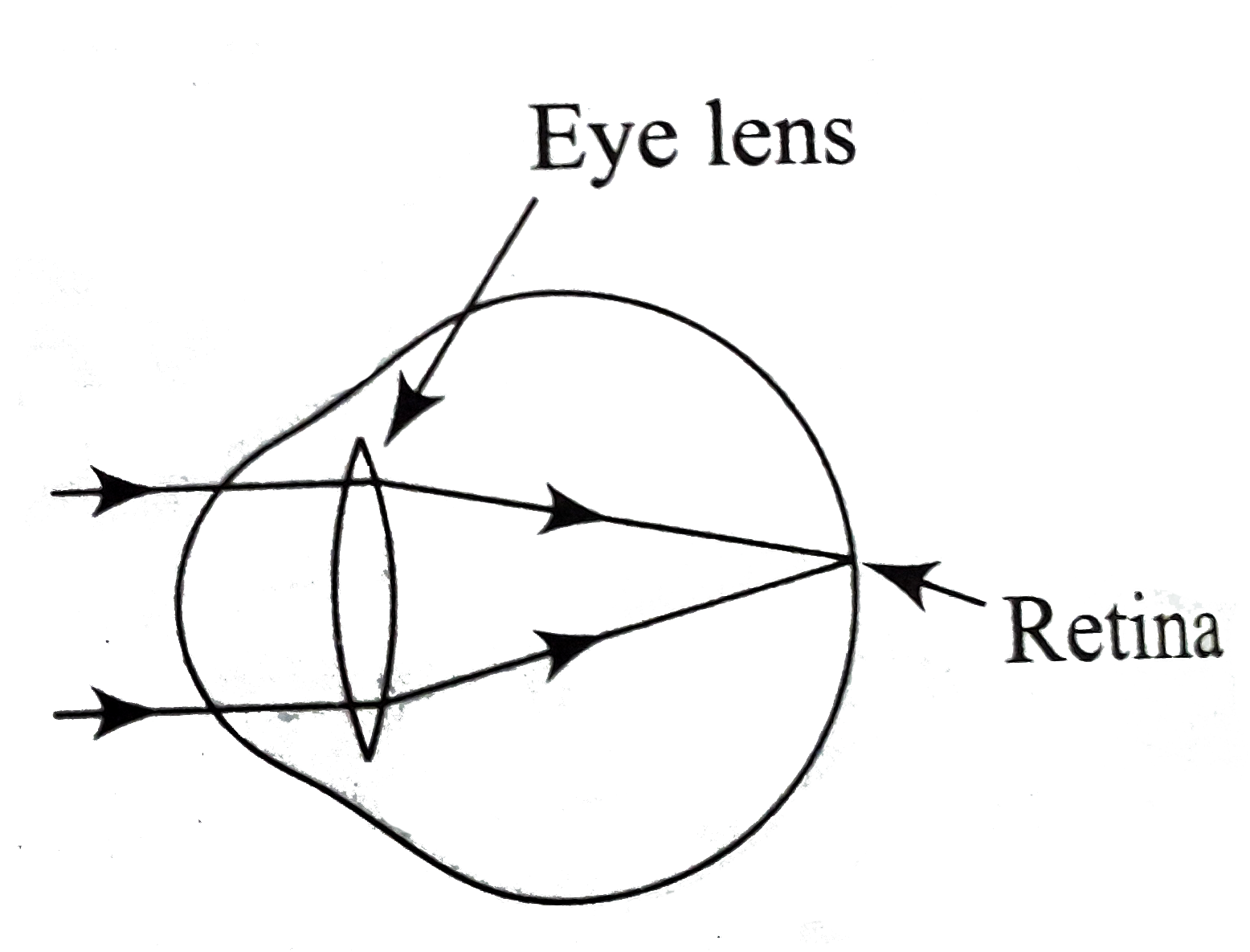
Q. A near sighted man can clearly see ojects only upto a distance of 100cm and not beyond this. The number of the spectacle lenses necessary for the remedy of this defect will beView SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
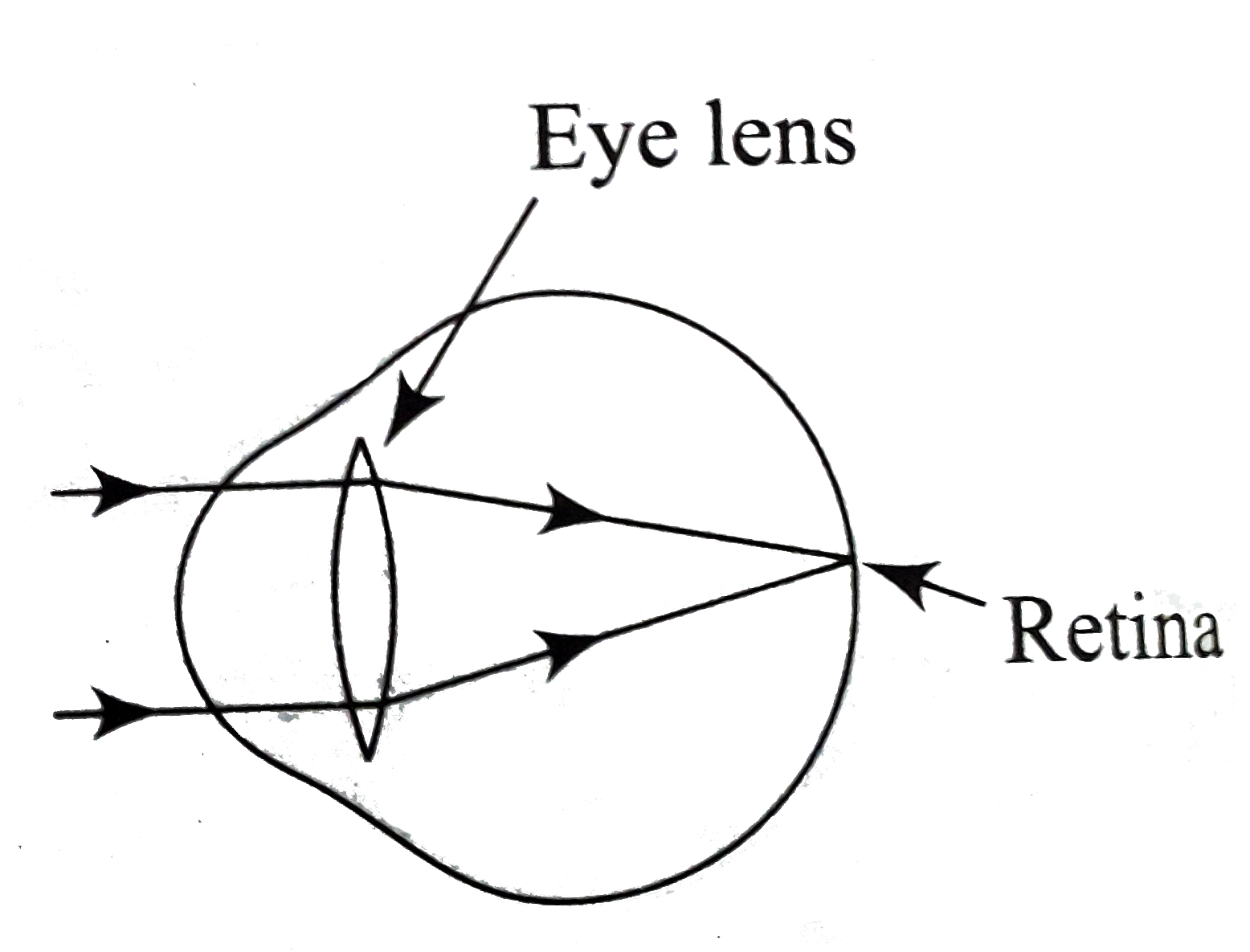
Q. A far sighted man connot see objects clearly unless they are at least 100cm from his eyes. The number of the spectacle lenses that will make his range of clear vision equal to an average grown up person will beView Solution

