A line cuts the x-axis at A(7,0) and the y-axis at B(0,−5) A variable line PQ is drawn perpendicular to AB cutting the x-axis in P and the y-axis in Q. If AQ and BP intersect at R, find the locus of R.
From the figure in ΔABQ,
AP⊥BQ,PQ⊥AB

Then, we have Bp⊥AQ (as the altitudes of triangle are concurrent). Hence,
BR⊥AR
or k−0h−7×k+5h−0=−1
Therefore, equation of the locus of R is x2+y2−7x+5y=0 .
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Concept applications 1.1
6 Videos
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Concept applications 1.2
8 Videos
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.67
1 Videos
- COORDINATE SYSTEMBOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE ENGLISHCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
A line intersects x-axis at A(2,0) and y-axis at B(0,4). A variable lines PQ which is perpendicular to AB intersects x-axis at P and y-axis at Q. AQandBP intersect at R. Locus of R is : (A) x2+y2−2x+4y=0 (B) x2+y2+2x+4y=0 (C) x2+y2−2x−4y=0 (D) x2+y2+2x−4y=0
View SolutionThe line 2x+3y=12 meets the x-axis at A and y-axis at B. The line through (5,5) perpendicular to AB meets the x-axis and the line AB at C and E respectively. If O is the origin of coordinates, find the area of figure OCEB.
View Solution
Knowledge Check
The line xa−yb=1 cuts the x-axis at P. The equation of the line through P and perpendicular to the given line is
A(a) x+y=abB(b) x+y=a+bC(c) ax+by=a2D(d) bx+ay=b2
The line L1≡4x+3y−12=0 intersects the x-and y-axies at A and B, respectively. A variable line perpendicular to L1 intersects the x- and the y-axis at P and Q , respectively. Then the locus of the circumcenter of triangle ABQ is (a) 3x−4y+2=0 (b) 4x+3y+7=0 (c) 6x−8y+7=0 (d) none of these
View SolutionThe line L1≡4x+3y−12=0 intersects the x-and y-axies at AandB, respectively. A variable line perpendicular to L1 intersects the x- and the y-axis at P and Q , respectively. Then the locus of the circumcenter of triangle ABQ is (a) 3x−4y+2=0 (b) 4x+3y+7=0 (c) 6x−8y+7=0 (d) none of these
View SolutionThe straight line xa+yb=1 cuts the axes in A and B and a line perpendicular to AB cuts the axes in P and Q. Find the locus of the point of intersection of AQ and BP .
View SolutionLet a line xa+yb=1 intersects the x-axis at A and y-axis at B resapectively. A line parallel to it is drawn to intersect the axes in P and Q respectively. The extermities of the lines are joined transversely. If the locus of point of intersection of the line joining them is xa=cyb, then c is equal to
View SolutionA line through point P(4, 3) meets x-axis at point A and the y-axis at point B. If BP is double of PA, find the equation of AB.
View SolutionA line AB meets X-axis at A and Y-axis at B. P(4,−1) divides AB in the ratio 1:2.
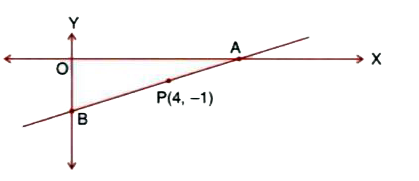
Find the Coordinates of A and B
View SolutionThe line through A(4, 7) with gradient m meets the x-axis at P and the y-axis at R. The line through B(8, 3) with gradient −1m meets the x-axis at Q and the y-axis at S. Find in term of m, the co-ordinates of P, Q, R and S. Obtain expressions for OP. OQ and OR. OS, where O is the point (0, 0).
View Solution
