A line is drawn perpendicular to line y=5x, meeting the coordinate axes at AandB . If the area of triangle OAB is 10 sq. units, where O is the origin, then the equation of drawn line is (a) 3x−y−9 (b) x+5y=10 x+4y=10 (d) x−4y=10
12
-12
10
-10
The correct Answer is:A, B
Let the equation of line be xa+yb=1.
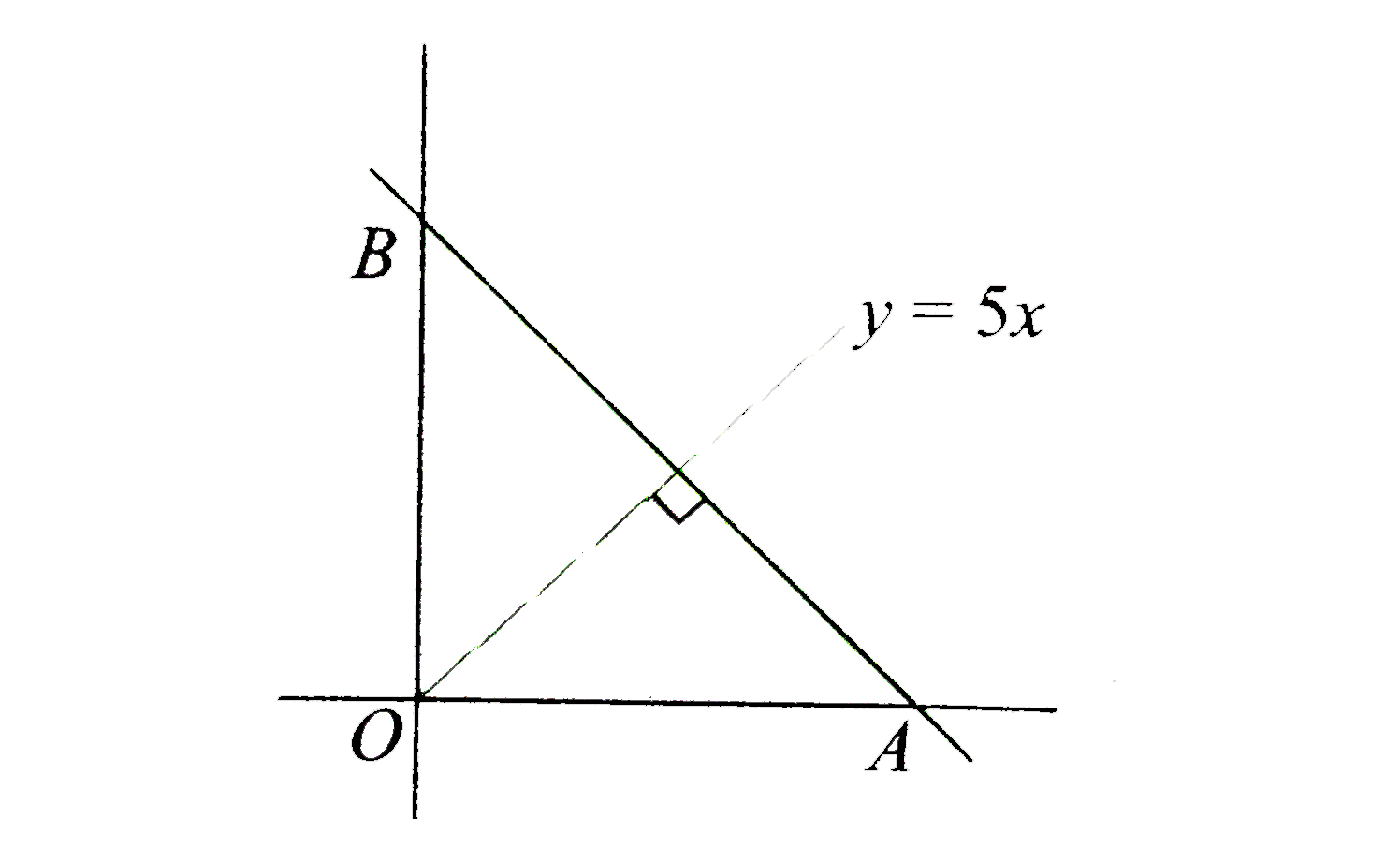
AB is perpendicular to y = 5x.
∴−ba×5=−1 or 5b=a
Area of ΔOAB=12|ab|
⇒10=12∣∣5b2∣∣
⇒b2=4
⇒b=±2
When b=2, a=10 " and when" b =-2, a=-10.
The line can be x10+y2=1 or x10+y2=−1.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)27videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MATRIX MATCH TYPE)8videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (SINGLE CORRECT ANSWER TYPE)82videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
A line is drawn perpendicular to line y=5x, meeting the coordinate axes at AandB . If the area of triangle OAB is 10 sq. units, where O is the origin, then the equation of drawn line is 3x−y−9 (b) x−5y=10 x+4y=10 (d) x−4y=10
View SolutionIf a line is perpendicular to the line 5x−y=0 and forms a triangle with coordinate axes of area 5 sq. units, then its equation is :
View SolutionA line is drawn perpendicular to5x=y+7. Find the equation of lines if the area of the triangle formed by this line with coordinate axes is 5sq. Units.
View SolutionA straight line L is perpendicular to the line 5x−y=1. The area of the triangle formed by the line L and the coordinate axes is 5'□units.F∈dtheequationofthel∈eL
View SolutionIf x−2y+4=0and2x+y−5=0 are the sides of an isosceles triangle having area 10sq.units , the equation of the third side is (a) 3x−y=−9 (b) 3x−y+11=0 (c) x−3y=19 (d) 3x−y+15=0
View SolutionFind the equation of a line drawn perpendicular to the line x4+y6=1 through the point where it meets the y axis.
View SolutionFind the equation of a line drawn perpendicular to the line x4+y6=1 through the point where it meets the y axis.
View SolutionThe line x6+y8=1 cuts the co-ordinate axis at A & B . If O is origin, then ∏sinA2 for the triangle OAB is 56 (b) 110 (c) 54 (d) none of these
View SolutionA straight line is drawn through P(3,4) to meet the axis of x and y at AandB , respectively. If the rectangle OACB is completed, then find the locus of C.
View SolutionA line passes through (−3,4) and the portion of the line intercepted between the coordinate axes is bisected at the point then equation of line is (A) 4x−3y+24=0 (B) x−y−7=0 (C) 3x−4y+25=0 (D) 3x−4y+24=0
View Solution

