A line L1≡3y−2x−6=0 is rotated about its point of intersection with the y-axis in the clockwise direction to make it L2 such that the are formed by L1,L2 the x-axis, and line x=5 is 493sq.units if its point of intersection with x=5 lies below the x-axis. Find the equation of L2.
The correct Answer is:x+y=2
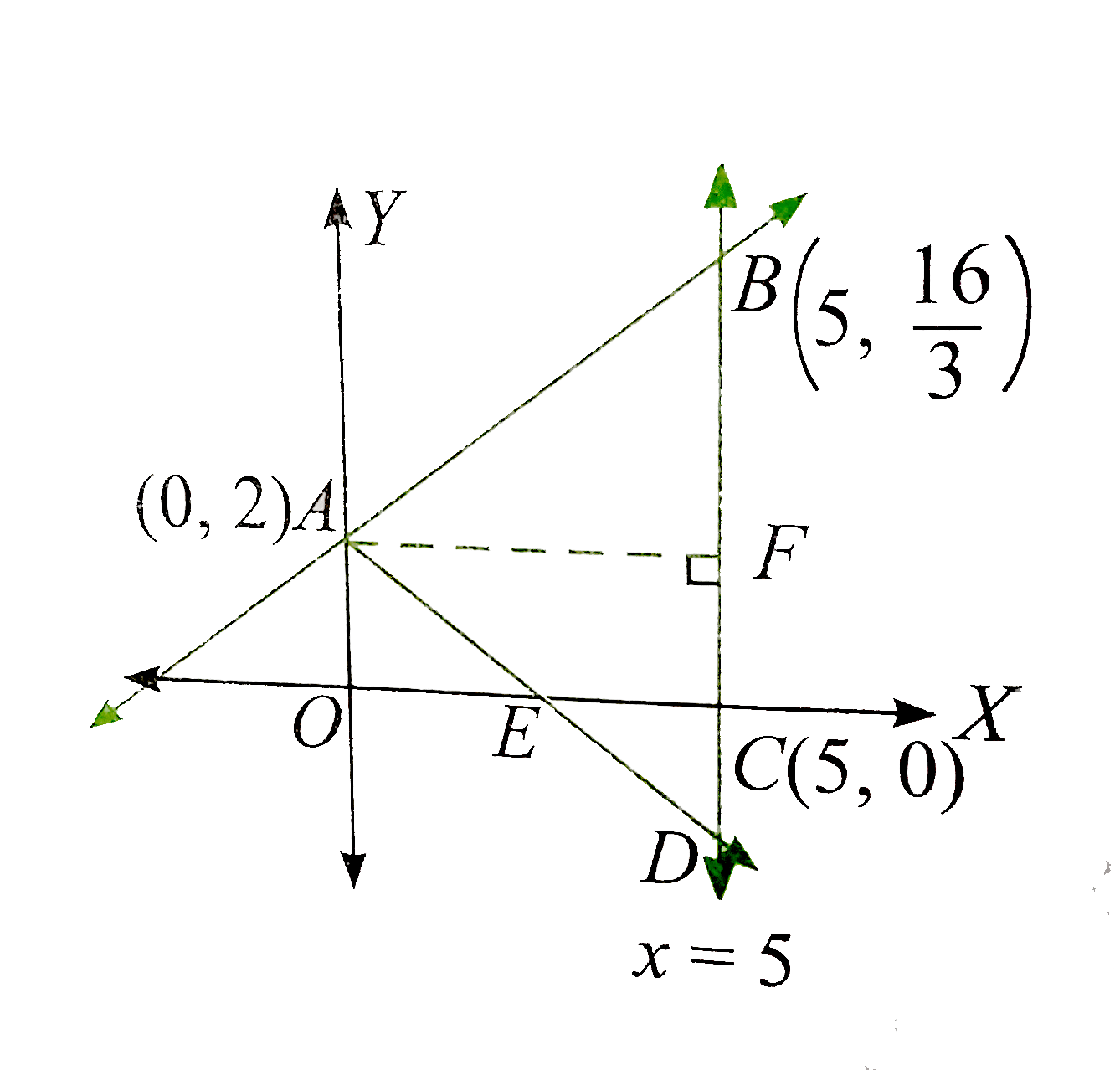
L1=3y−2x−6=0
The point about which the line is rotated is A = (0,2). Let the equation of L2 be y = mx +2. As L2 will be cutting line x=5 below the x-axis, we have
A≡(0,2),B≡(5,163),C≡(5,0),
D≡(5,5m+2),E≡(−2m,0)
Now, Area of AECB= Area of ΔADB−Area of ΔECD
or 493=12BD×AF−12EC×CD
=12[163−(5m+2)]×5−12×(5+2m)[−(5m+2)]
or 493=110m+126mor m=−1
Hence, the equation of L2 is x+y=2.
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.2
4 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.3
7 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXAMPLE
12 Videos
- STRAIGHT LINEBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )
1 Videos
Similar Questions
Find the point of intersection of the lines 2x−3y+8=0 and 4x+5y=6
View SolutionFind the point of intersection of the circle x2+y2−3x−4y+2=0 with the x-axis.
View SolutionA line intersects x-axis at point (-2, 0) and cuts off an intercept of 3 units from the positive side of y-axis. Find the equation of the line.
View SolutionThe lines L1:x−2y+6=0&L2:x−2y−9=0 are tangents to the same circle. If the point of contact of L1 with the circle is (−2,2), then: the centre of the circle is (−72,5) the centre of the circle is (−12,−1) area of the circle is 45π4sq.untis the point of contact of L2 with the circle has the co-ordinates (−5,8)
View SolutionLying in the plane x+y+z=6 is a line L passing through (1, 2, 3) and perpendicular to the line of intersection of planes x+y+z=6 and 2x−y+z=4, then the equation of L is
View SolutionA straight line L through the point (3,-2) is inclined at an angle 60∘ to the line √3x+y=1. If L also intersects the x-axis then find the equation of L .
View SolutionThe equation of line l1 is y=2x+3, and the equation of line l2 is y=2x-5.
View SolutionLet L be the line 2x+y−2=0. The axes are rotated by 45∘ in clockwise direction then the intercepts made by the line L on the new axes are respectively
View SolutionThe point of intersection of tangents drawn to the hyperbola x2a2−y2b2=1 at the points where it is intersected by the line lx+my+n=0 is
View SolutionThe plane lx+my=0 is rotated through an angle α about its line of intersection with the plane z=0 . Prove that the equation of the plane in its new position is lx+my±(√l2+m2tanα)z=0.
View Solution
