A line OA of length r starts from its initial position OX and traces an angle AOB = α in the anitclockwise direction. It then traces back in the clockwise direction an angle BOC = 3θ ( where α>3θ). L is the foot of the perpendicular from C on OA. Also, sin3θCL=cos3θOL=1
1−rcosαrsinα is equal to Solution in Tamil
tan2θ
cot2θ
sin2θ
sin2θ
The correct Answer is:A
OL=rcos(α−3θ)
CL=rsin(α−3θ)

So, sin3θrsin(α−3θ)=cos3θrcos(α−3θ)=1
⇒sin3θsin(α−3θ)=cos3θcos(α−3θ)=r
Now cos4θ−sin4θ
=cosθ(rcos(α−3θ))−sinθ(rsin(α−3θ))
⇒cos2θ=rcos(α−2θ)
⇒cos2θ=r(cosαcos2θ+sinαsin2θ)
⇒(1−rcosα)cos2θ=rsinαsin2θ
⇒(1−rcosα)cos2θ=rsinαsin2θ ...(1)
cos3θsinθ+sin3θcosθ
=r[cos(α−3θ)sinθ+sin(α−3θ)cosθ]
⇒sinθcosθ=rsin(α−2θ)
⇒sin2θ=2r[sinαcos2θ−cosαsin2θ]
⇒(1+2rcosα)sin2θ=2rsinαcos2θ
⇒1+2rcosα2rsinα=cot2θ ...(2)
From (1) and (2), we get
1−rcosαrsinα=2rsinα1+2rcosα
⇒1−rcosα+2rcosα−2r2cos2α=2r2sin2α
⇒2r2−1r=cosα
Topper's Solved these Questions
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Exercise (Matrix Match Type )
9 Videos
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Exercise (Numerical)
38 Videos
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Exercise (Multiple)
22 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - SINGLE CORRECT ANSWER TYPE
38 Videos
- TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS BOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS EXERCISE - Multiple Correct Answers Type
6 Videos
Similar Questions
If cosθ−sinθ=15, where 0<θ<π4, then

View SolutionIf f(θ)=1−sin2θ+cos2θ2cos2θ , then value of 8f(110)f(340) is ____
View SolutionIf cosβ is the geometric mean between sinαandcosα, where 0<α,β<π2, then cos2β is equal to −2sin2(π4−α) (b) −2cos2(π4+α) −2s∈2(π4+α) (d) 2cos2(π4−α)
View SolutionThe circular wire of diameter 10 cm is cut and placed along the circumference of a circle of diameter 1 meter. The angle subtended by the wire at the centre of circle is equal to
View SolutionIf sec x + tan x =22/7 , find the value of tanx/2
View SolutionIf sin alpha=(1)/(2) and cos theta=(1)/(3) then the values of alpha+theta( if theta,alpha are both acute angles) will lie in the interval
View Solutionsin(3 theta+alpha)+sin(3 theta-alpha)+sin(alpha-theta)-sin(alpha+theta)=cos alpha
View SolutionA line OA of length r starts from its initial position OX and traces an angle AOB = α in the anitclockwise direction. It then traces back in the clockwise direction an angle BOC = 3θ ( where α>3θ). L is the foot of the perpendicular from C on OA. Also, sin3θCL=cos3θOL=1
1−rcosαrsinα is equal to
View SolutionA line OA of length r starts from its initial position OX and traces an angle AOB = α in the anitclockwise direction. It then traces back in the clockwise direction an angle BOC = 3θ ( where α>3θ). L is the foot of the perpendicular from C on OA. Also, sin3θCL=cos3θOL=1
2rsinα1+2rcosα is equal to
View SolutionA line OA of length r starts from its initial position OX and traces an angle AOB = α in the anitclockwise direction. It then traces back in the clockwise direction an angle BOC = 3θ ( where α>3θ). L is the foot of the perpendicular from C on OA. Also, sin3θCL=cos3θOL=1
2r2−1r is equal to
View SolutionLet OP=rand∠XOP=θ then the position of P in polar coordinate system is represented by (r,θ) OX and O are called the initial line and pole respectively.
If p be the length of perpendicular from origin to line and if α is the angle which the perpendicular to the line makes with the initial line . The equation of line is given by r cos (θ−α)=p
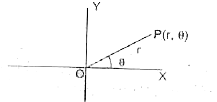
Perpendicular distance from pole to the line lr=4cosθ+2sinθ is
View SolutionA line OA of length r starts from its initial position OX and traces an angle AOB = α in the anitclockwise direction. It then traces back in the clockwise direction an angle BOC = 3θ ( where α>3θ). L is the foot of the perpendicular from C on OA. Also, sin3θCL=cos3θOL=1
2rsinα1+2rcosα is equal to
View SolutionA line OA of length r starts from its initial position OX and traces an angle AOB = α in the anitclockwise direction. It then traces back in the clockwise direction an angle BOC = 3θ ( where α>3θ). L is the foot of the perpendicular from C on OA. Also, sin3θCL=cos3θOL=1
2r2−1r is equal to
View SolutionA line OA length r starts from its initial position OX and traces an angle AOB=α in the anticlockwise direction. It then traces back in the clockwise direction an angle BOC=3θ ( where α>3θ ) . L is the foot of the the perpendicular from C on OA. sin3θCL=cos3θOL=1
1−rcosαrsinα is equal to
View SolutionA line OA length r starts from its initial position OX and traces an angle AOB=α in the anticlockwise direction. It then traces back in the clockwise direction an angle BOC=3θ ( where α>3θ ) . L is the foot of the the perpendicular from C on OA. sin3θCL=cos3θOL=1
2rsinα1+2rcosα is equal to
View SolutionA line OA length r starts from its initial position OX and traces an angle AOB=α in the anticlockwise direction. It then traces back in the clockwise direction an angle BOC=3θ ( where α>3θ ) . L is the foot of the the perpendicular from C on OA. sin3θCL=cos3θOL=1
1−rcosαrsinα is equal to
View Solution
