A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the tune (in minutes) required for each toy on the machines is given below:Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs 7.50 and that on each toy of type B is Rs 5. show that 15 toys of type A and 30 of the B should be manufactured m a day to get maximum profit.
To solve the problem of maximizing profit from manufacturing toys A and B, we will follow these steps:
Step 1: Define Variables
Let:
- x = number of toys of type A produced
- y = number of toys of type B produced
Step 2: Profit Function
The profit from producing toys A and B can be expressed as:
Z=7.5x+5y
where Z is the total profit.
Step 3: Identify Constraints
Each machine is available for a maximum of 6 hours per day, which translates to 360 minutes. The time required for each toy on the machines is given as follows:
- Machine 1:
- Toy A: 12 minutes
- Toy B: 6 minutes
- Constraint:
12x+6y≤360(1)
- Machine 2:
- Toy A: 18 minutes
- Toy B: 2 minutes
- Constraint:
18x+2y≤360(2)
- Machine 3:
- Toy A: 2 minutes
- Toy B: 3 minutes
- Constraint:
2x+3y≤360(3)
Step 4: Non-negativity Constraints
We also need to ensure that the number of toys produced cannot be negative:
x≥0,y≥0(4)
Step 5: Solve the Constraints
We will solve the inequalities to find the feasible region.
1. From constraint (1):
12x+6y≤360⟹2x+y≤60(5)
2. From constraint (2):
18x+2y≤360⟹9x+y≤180(6)
3. From constraint (3):
2x+3y≤360(7)
Step 6: Find Intersection Points
To find the corner points of the feasible region, we will solve the equations obtained from the constraints.
- Intersection of (5) and (6):
2x+y=60(8)
9x+y=180(9)
Subtract (8) from (9):
7x=120⟹x=17.14(not feasible)
- Intersection of (5) and (7):
2x+y=60(8)
2x+3y=360(10)
From (8), y=60−2x. Substitute into (10):
2x+3(60−2x)=360⟹2x+180−6x=360⟹−4x=180⟹x=45(not feasible)
- Intersection of (6) and (7):
9x+y=180(9)
2x+3y=360(10)
From (9), y=180−9x. Substitute into (10):
2x+3(180−9x)=360⟹2x+540−27x=360⟹−25x=−180⟹x=7.2
Substitute x back into (9):
y=180−9(7.2)=180−64.8=115.2(not feasible)
Step 7: Evaluate Corner Points
We can evaluate the feasible corner points (0, 60), (15, 30), (20, 20), and (20, 0) to find the maximum profit.
1. For (0,60):
Z=7.5(0)+5(60)=300
2. For (15,30):
Z=7.5(15)+5(30)=112.5+150=262.5
3. For (20,20):
Z=7.5(20)+5(20)=150+100=250
4. For (20,0):
Z=7.5(20)+5(0)=150
Step 8: Conclusion
The maximum profit of Rs 262.5 occurs when 15 toys of type A and 30 toys of type B are produced.
Let:
- x = number of toys of type A produced
- y = number of toys of type B produced
The profit from producing toys A and B can be expressed as:
Z=7.5x+5y
where Z is the total profit.
Each machine is available for a maximum of 6 hours per day, which translates to 360 minutes. The time required for each toy on the machines is given as follows:
- Toy A: 12 minutes
- Toy B: 6 minutes
- Constraint:
12x+6y≤360(1)
- Toy A: 18 minutes
- Toy B: 2 minutes
- Constraint:
18x+2y≤360(2)
- Toy A: 2 minutes
- Toy B: 3 minutes
- Constraint:
2x+3y≤360(3)
We also need to ensure that the number of toys produced cannot be negative:
x≥0,y≥0(4)
We will solve the inequalities to find the feasible region.
12x+6y≤360⟹2x+y≤60(5)
18x+2y≤360⟹9x+y≤180(6)
2x+3y≤360(7)
To find the corner points of the feasible region, we will solve the equations obtained from the constraints.
2x+y=60(8)
9x+y=180(9)
Subtract (8) from (9):
7x=120⟹x=17.14(not feasible)
2x+y=60(8)
2x+3y=360(10)
From (8), y=60−2x. Substitute into (10):
2x+3(60−2x)=360⟹2x+180−6x=360⟹−4x=180⟹x=45(not feasible)
9x+y=180(9)
2x+3y=360(10)
From (9), y=180−9x. Substitute into (10):
2x+3(180−9x)=360⟹2x+540−27x=360⟹−25x=−180⟹x=7.2
Substitute x back into (9):
y=180−9(7.2)=180−64.8=115.2(not feasible)
We can evaluate the feasible corner points (0, 60), (15, 30), (20, 20), and (20, 0) to find the maximum profit.
Z=7.5(0)+5(60)=300
Z=7.5(15)+5(30)=112.5+150=262.5
Z=7.5(20)+5(20)=150+100=250
Z=7.5(20)+5(0)=150
The maximum profit of Rs 262.5 occurs when 15 toys of type A and 30 toys of type B are produced.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - NCERTCHAPTER - LINEAR PROGRAMMINGEXERCISE - EXERCISE 12.2
11 Videos
- LINEAR PROGRAMMINGBOOK - NCERTCHAPTER - LINEAR PROGRAMMINGEXERCISE - SOLVED EXAMPLES
11 Videos
- LINEAR PROGRAMMINGBOOK - NCERTCHAPTER - LINEAR PROGRAMMINGEXERCISE - SOLVED EXAMPLES
11 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - NCERTCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE
17 Videos
- MATRICESBOOK - NCERTCHAPTER - MATRICESEXERCISE - EXERCISE 3.3
12 Videos
Similar Questions
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each purpose and the time (in minutes) required for each toy on the machines is given below:
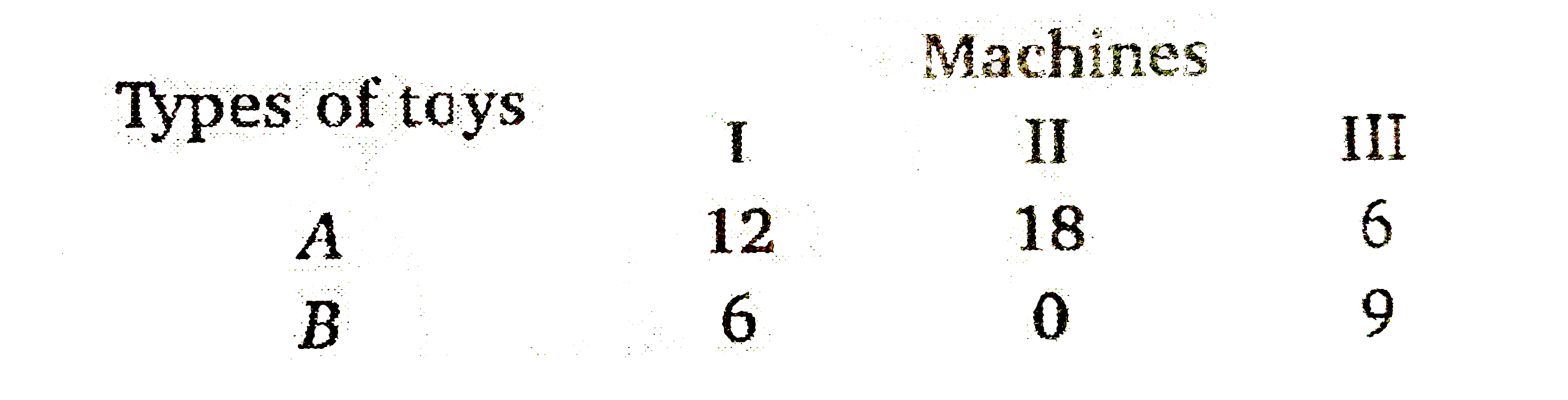
Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs. 7.50 and that on each toy of type B is Rs. 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
View SolutionA manufacturer makes two types of toys A and B.Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:

The machine I, II and III are available for a maximum of 3 hours, 2 hours and 2 hours 30 minutes respectively.The profit on each toy of type A is ₹ 50 and that of type B is ₹ 60.Formulate the above problem as a LPP and solve graphically to maximize profit.
View Solution
Knowledge Check
The cost of 24 toys of the same kind is Rs 783.60. Find the cost of each toy.
A31.65B32.00C32.65D30.65
A manufacture makes two types of cups A and B. Three machines are required to manufacture the cups and the time in minutes required by each in as given below:

Each machine is available for a maximum period of 6 hours per day. If the profit on each cup A is 75 paisa and on B is 50 paisa, find how many cups of each type should be manufactures to maximise the profit per day.
View SolutionA copany manufactures two types of toys, A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. The profit is Rs.50 each on type A and Rs.60 each on type B. How many toys of each type should the company manufacture in a day to maximize the profit?
View SolutionA company manufactures two types of toys A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. He earns a profit of Rs.50 each on type A and Rs.60 each on type. B. How many toys of each type should the company manufacture in a day to maximize the profit ?
View SolutionIn a small scale industry, a manufacturer produces two types of book cases. The first type of book case requires 3 hours on machine A and 2 hours on machine B for completion whereas the second type of book case requires 3 hours on machine A and 3 hours on machine B. The machines A and B respectively run for at the most 18 hours and 14 hours per day. He earns a profit of 30 on each type of case of first type and 40 on each book case of second type. How many book cases of each type should he manufacture so as to have maximum profit. Make it an LPP and solve it graphically.
View SolutionIf the cost of 9 toys is Rs 333.find the cost of one toy
View SolutionA company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours for assembling. The profit is Rs 5 each for type A and Rs 6 each for type B souvenirs. How many souvenirs of each type should the company manufacture m order to maximise the profit?
View SolutionA manufacturing company makes two types of teaching aids A and B . Each type of A requires 9 labour hours for fabricating and 1 labour hours for finishing.Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing.For fabricating and finishing, the maximum labour hours abailable per week are 180 and 30 respectively.The company makes a profit of ₹ 80 on each type A and ₹ 120 on each type B. How many pieces of type A and type B should be manufactured per week to get a maximum profit? Make it as an LPP and solve graphically.What is the maximum profit per week?
View Solution
