A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs 17.50 per package on nuts and Rs 7.00 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machine for at most 12 hours a day?
Let the manufacturer produces x packets of nuts and y packets of bolts, then
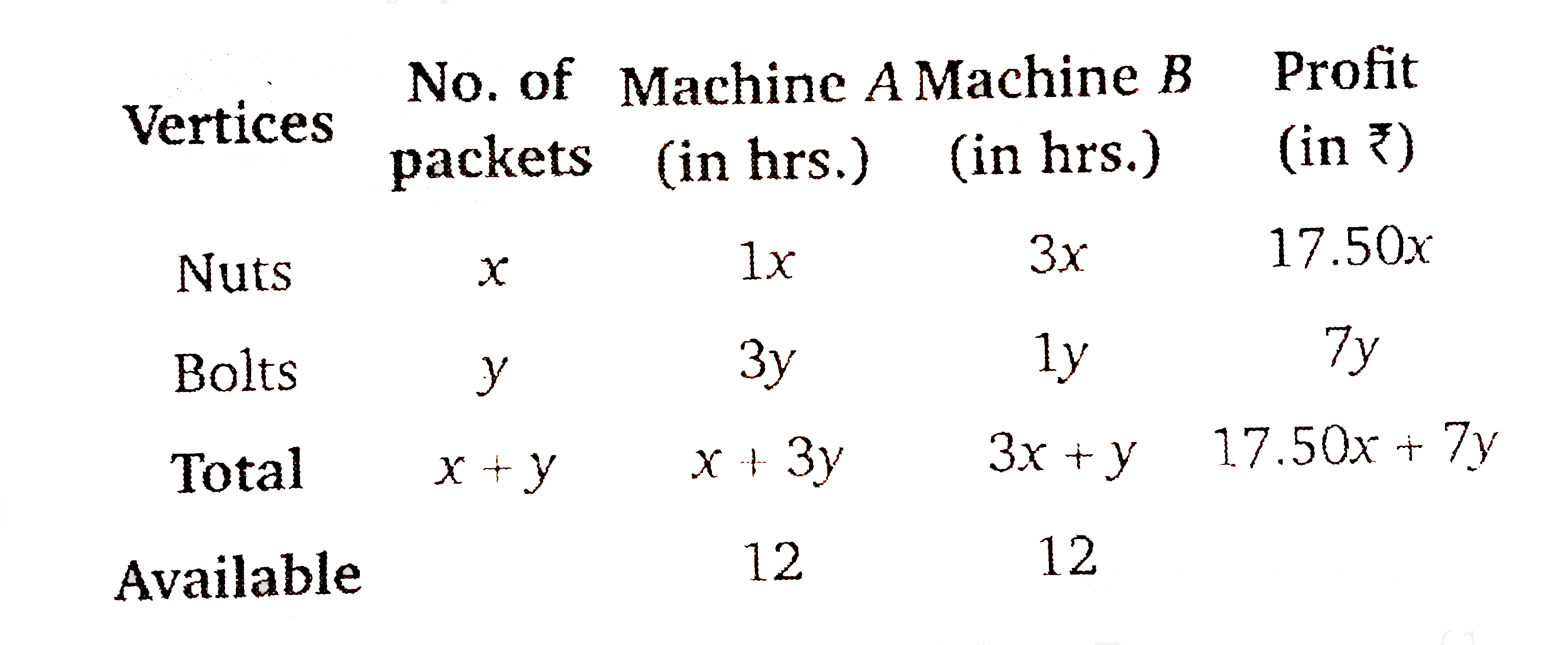
∴ Maximise Z=17.5x+7y……………….1
and constraints x+3y≤12………………………2
3x+y≤12………………….3
x≥0,y≥0………………...4

First draw the graph of the line x+3y=12.
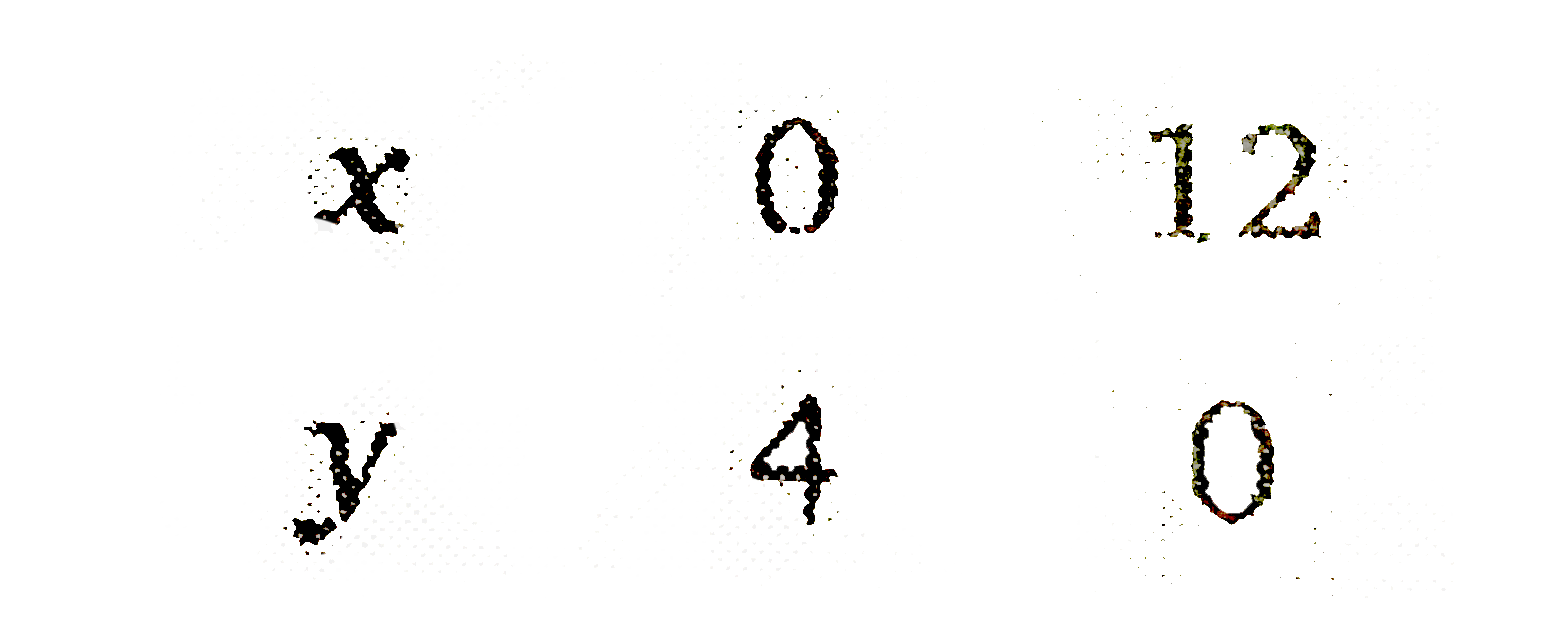
Put (0,0) in the inequation x+3y≥12 ,
0+3×0≤10⇒0≤12 (True)
Therefore half plane contains the origin. Since x,y≥0. So the feasible region is in first quadrant,
Now draw the graph of the line 3x+y=12
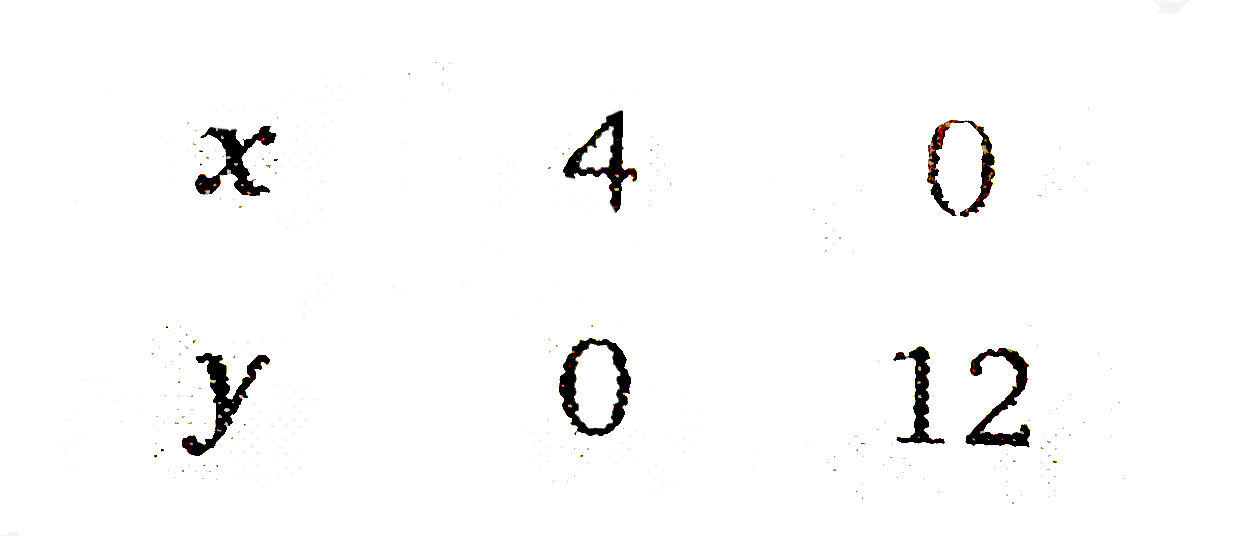
Put (0,0) in the inequation 3x+y≤12,
3×0+0≤12>0≤12 (True)
Therefore, the half plane contains the origin.
From the equations x+3y=12 and 3x+y=12, the point of intersection is B(3,3).
∴ The feasible region is OABCO whose vertices are O(0,0),A(4,0),B(3,3) and C(0,4). Now, we find the value of Z at these points,
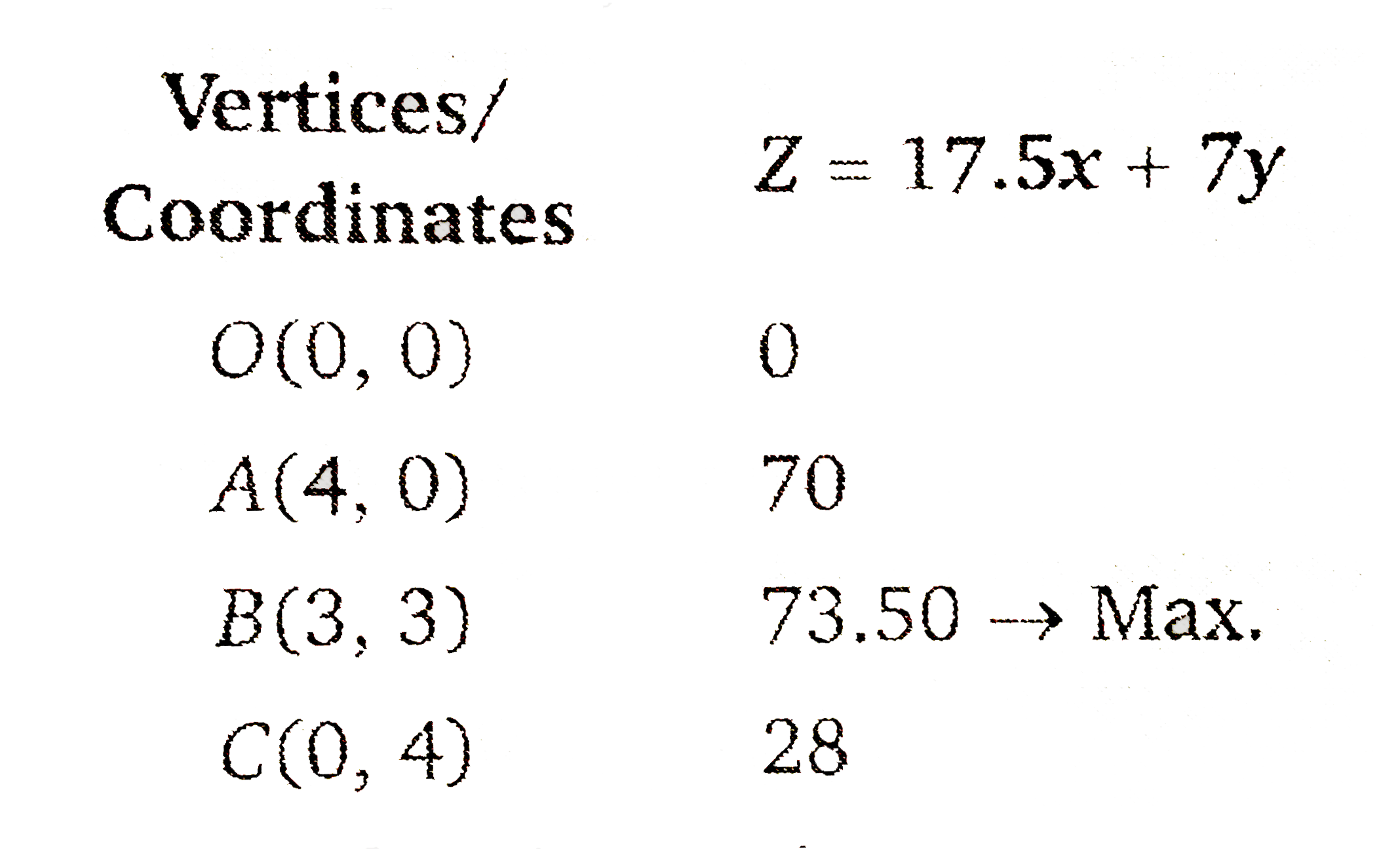
The value of Z is maximum Rs. 73.50 at point (3,3). Therefore, the maximum profit of Rs. 73.50 can be obtained when 3 packets of nuts and 3 packets of bolts are produced per day.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - Miscellaneous Exercise
9 Videos
- LINEAR PROGRAMMINGBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12.1
10 Videos
- INVERES TRIGONOMETRIC FUNCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INVERES TRIGONOMETRIC FUNCTIONSEXERCISE - Miscellaneous Exercise (prove That )
9 Videos
- MATRICESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - MATRICESEXERCISE - Miscellaneous Exerice
15 Videos
Similar Questions
A manufacturer produces nuts and bolts. It takes 2 hours work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 2 hours on machine B to produce a package of bolts. He earns a profit of Rs. 24 per package on nuts and Rs. 18 per package on bolts. How many packages of each should be produced each day so as to maximize his profit, if he operates his machines for at the most 10 hours a day. Make an L.P.P. from above and solve it graphically ?
View SolutionA manufacturer produces two types of steel trunks. He has tow machines A and B. For completing, the first types of the trunk requires 3 hours on machine A and 3 hours on machine B, whereas the second type of the trunk requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs. 30 and Rs. 25 per trunk of the first type and the second respectively. How many trunks of each type must he make each day to makes maximum profit?
View SolutionA small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes 1 hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is Rs 100 and that on a bracelet is Rs 300, how many of each should be produced daily to maximize the profit?
View SolutionManufacturer produces two types of steel trunks. He has two machines, A and B. The first type of trunk requires 3 hours on machine A and 3 hours on machine B. The second type requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs. 30 per trunk on the first type of trunk and Rs. 25 per trunk on the second type. Formulate a linear programming problem to find out how many trunks of each type he must make each day to maximize his profit.
View SolutionA factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of 70 paise and screws B at a profit of Rs 1. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit? Formulate the above LPP and solve it graphically and determine the maximum profit.
View SolutionA factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of 70 paise and screws B at a profit of Rs 1. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit? Formulate the above LPP and solve it graphically and determine the maximum profit.
View SolutionA furniture form manufactures chairs and tables, each requiring the use of three machines A, B and C. Production of one chair requires 2 hours on machine A, 1 hour on machine B, and 1 hour on machine C. Each table requires 1 hour each on machines A and B and 3 hours on machine C. Profit realized by selling one chair is Rs. 30 while for a table the figure is Rs. 60. The total time available per week on machine A is 70 hours, on machine B is 40 hours, and on machine C is 90 hours. How many chairs and table should be made per week so as to maximize profit? Develop a mathematical formulation.
View SolutionA factory manufactures two types of screws, A and B, each type requiring the use of two machines, an automatic and a hand-operated. It takes 4 minutes on the automatic and 6 minutes on hand-operated machines to manufacture a packet of screws 'A', while it takes 6 minutes on the automatic and 3 minutes on the hand-operated machines to manufacture a packet of screws 'B'. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a packet of screws 'A' at a profit of 70 paise and screws 'B' at a profit of Rs. 1. Assuming that he can sell all the screws he manufactures, how many packets of each type should the factory owner produce in a day in order to maximise his profit ? Formulate the above L.P.P. and solve it graphically and find the maximum profit.
View SolutionCarina has 100 ounces of coffee divided into 5 - and 10 - ounce packages. If she has 2 more 5 - ounce packages than 10 - ounce packeages, how many 10 - ounce packages does she have?
View SolutionA factory requires 42 machines to produce a given number of articles in 63 days. How many machines would be required to produce the same number of articles in 54 days?
View Solution
