If a pair of perpendicular straight lines drawn through the origin forms an isosceles triangle with the line , then area of the triangle so formed is 36/13 (b) 12/17 (c) 13/5 (d) 17/14
The correct Answer is:A
As shown in the following figure, pair of perpendicular lines through origin meets given line 2x+3y=6 at A and B such that AOB is right angled isosceles triangle.
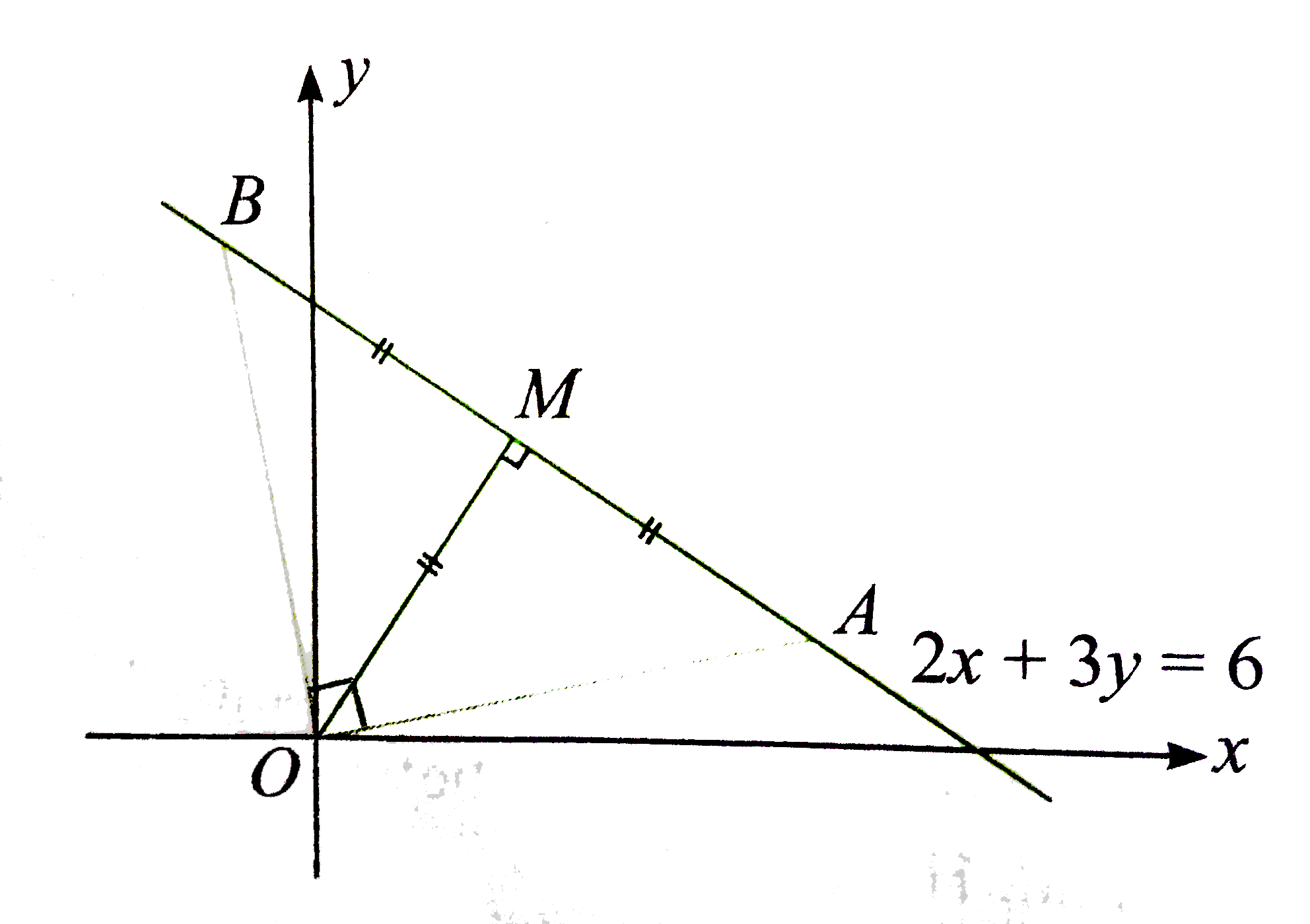
Now, OM=BM=AM, where OM
sq. units.
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Multiple)
30 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Comprehension)
27 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.6
5 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
If a pair of perpendicular straight lines drawn through the origin forms an isosceles triangle with the line 2x+3y=6 , then area of the triangle so formed is (a) 3613 (b) 1217 (c) 135 (d) 1714
View SolutionTwo mutually perpendicular straight lines through the origin from an isosceles triangle with the line 2x+y=5. Then the area of the triangle is
View Solution
Knowledge Check
A pair of straight lines drawn through the origin form with the line 2x+3y=6 an isosceles right angled triangled then the sides and the area of the triangle thus formed is
Ax−5y=0
5x+y=0
Δ=3613B3x−y=0
x+3y=0
Δ=1217C5x−y=0
x+5y=0
D≤ta=135DNoneDrawn from origin are two mutually perpendicular lines forming an isosceles triangle together with the straight line 2x+y=a then the area of this triangle is
Aa22 sq unitsBa23 sq unitsCa25 sq unitsDNone of theseThe joint equation of pair of lines through the origin and making an equilateral triangle with the line 3x+4y=5, is
A39x2+48xy+11y2=0B39x2−48xy+11y2=0C39x2+96xy+11y2=0D39x2−96xy+11y2=0
A pair of perpendicular straight lines is drawn through the origin forming with the line 2x+3y=6 an isosceles triangle right-angled at the origin. The equation to the line pair is 5x2−24xy−5y2=0 5x2−26xy−5y2=0 5x2+24xy−5y2=0 5x2+26xy−5y2=0
View SolutionCombined equation of the two lines passing through the origin, forming an equilateral triangle with the line x+y+√3=0 is
View SolutionTwo lines are drawn through (3,4), each of which makes angle of 45∘ with the line x−y=2. Then area of the triangle formed by these lines is
View SolutionConsider the lines y=3x,y=6x and y=9
What is the area of the triangle formed by these lines ?
View SolutionConsider the lines y = 3x , y = 6x , y = 9
What is the area of the triangle formed by these lines ?
View Solution
