A particle moves along the parabola y2=2ax in such a way that its projection on y-axis has a constant velocity. Show that its projection on the x-axis moves with constant acceleration
constant velocity
constant acceleration
variable velocity
variable acceleration
The correct Answer is:B
To solve the problem step by step, we will analyze the motion of a particle along the parabola defined by the equation y2=2ax. We will show that if the projection of the particle on the y-axis has a constant velocity, then its projection on the x-axis moves with constant acceleration.
Step 1: Understand the given equation
The equation of the parabola is given by:
y2=2ax
This relates the coordinates x and y of the particle.
Step 2: Differentiate the equation with respect to time t
To find the relationship between the velocities in the x and y directions, we differentiate both sides of the equation with respect to time t:
ddt(y2)=ddt(2ax)
Using the chain rule, we get:
2ydydt=2adxdt
Dividing both sides by 2, we have:
ydydt=adxdt
Step 3: Express dydt in terms of dxdt
From the equation derived, we can express dydt:
dydt=aydxdt
Step 4: Differentiate again with respect to time t
Next, we differentiate dydt with respect to time t to find the acceleration:
d2ydt2=ddt(aydxdt)
Using the product rule, we get:
d2ydt2=ayd2xdt2+dxdtddt(ay)
Now, we need to differentiate ay:
ddt(ay)=−ay2dydt
Substituting this back into our equation gives:
d2ydt2=ayd2xdt2−ay2dydtdxdt
Step 5: Use the condition of constant velocity in the y-direction
Since it is given that the projection on the y-axis has a constant velocity, we have:
dydt=k(constant)
Thus, d2ydt2=0. Substituting this into our equation gives:
0=ayd2xdt2−ay2kdxdt
Step 6: Rearranging the equation
Rearranging the above equation leads to:
ayd2xdt2=ay2kdxdt
Multiplying through by y gives:
d2xdt2=kydxdt
Step 7: Show that d2xdt2 is constant
Since k is constant and y is a function of x (from the parabola equation), we can express y in terms of x:
y=√2ax
Substituting this into the equation shows that d2xdt2 is proportional to a constant, thus indicating that the acceleration in the x-direction is constant.
Conclusion
We have shown that if the projection of the particle on the y-axis moves with constant velocity, then the projection on the x-axis moves with constant acceleration.
The equation of the parabola is given by:
y2=2ax
This relates the coordinates x and y of the particle.
To find the relationship between the velocities in the x and y directions, we differentiate both sides of the equation with respect to time t:
ddt(y2)=ddt(2ax)
Using the chain rule, we get:
2ydydt=2adxdt
Dividing both sides by 2, we have:
ydydt=adxdt
From the equation derived, we can express dydt:
dydt=aydxdt
Next, we differentiate dydt with respect to time t to find the acceleration:
d2ydt2=ddt(aydxdt)
Using the product rule, we get:
d2ydt2=ayd2xdt2+dxdtddt(ay)
Now, we need to differentiate ay:
ddt(ay)=−ay2dydt
Substituting this back into our equation gives:
d2ydt2=ayd2xdt2−ay2dydtdxdt
Since it is given that the projection on the y-axis has a constant velocity, we have:
dydt=k(constant)
Thus, d2ydt2=0. Substituting this into our equation gives:
0=ayd2xdt2−ay2kdxdt
Rearranging the above equation leads to:
ayd2xdt2=ay2kdxdt
Multiplying through by y gives:
d2xdt2=kydxdt
Since k is constant and y is a function of x (from the parabola equation), we can express y in terms of x:
y=√2ax
Substituting this into the equation shows that d2xdt2 is proportional to a constant, thus indicating that the acceleration in the x-direction is constant.
We have shown that if the projection of the particle on the y-axis moves with constant velocity, then the projection on the x-axis moves with constant acceleration.
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Section I - Solved Mcqs27videos
DERIVATIVE AS A RATE MEASURER
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 256videos
DEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Chapter Test30videos
DIFFERENTIAL EQUATIONS
Similar Questions
A particle moves along a parabolic path y=−9x2 in such a way that the x component of velocity remains constant and has a value 13m/s. Find the instantaneous acceleration of the projectile (in m/s2)
View SolutionA particle moves along the parabolic path x=y2+2y+2 in such a way that Y-component of velocity vector remains 5ms−1 during the motion. The magnitude of the acceleration of the particle is
View SolutionA particle of mass m moves along a curve y=x2. When particle has x-coordinate as 12 m and x-component of velocity as 4ms, then
View SolutionA particle moves along a path y=ax2 (where a is constant) in such a way that x-component of its velocity (ux) remains constant. The acceleration of the particle is
View SolutionThe parabola having its focus at (3,2) and directrix along the Y-axis has its vertex at
View SolutionA particle moves along x - axis in such a way that its x - co - ordinate varies with time according to the equation x=4−2t+t2. The speed of the particle will vary with time as
View SolutionA particle moves along the x-axis in such a way that its x-co-ordinate varies with time as x=2–5t+6t2.
The initial velocity and acceleration of particle will respectively be-View SolutionThe velocity v of a particle moving along x - axis varies with ist position (x) as v=α√x, where α is a constant. Which of the following graph represents the variation of its acceleration (a) with time (t)?
View SolutionA particle is projected in air at some angle to the horizontal, moves along parabola as shown in figure where x and y indicate horizontal and vertical directions, respectively . Shown in the diagram, direction of velocity and acceleration at points A, B and C.
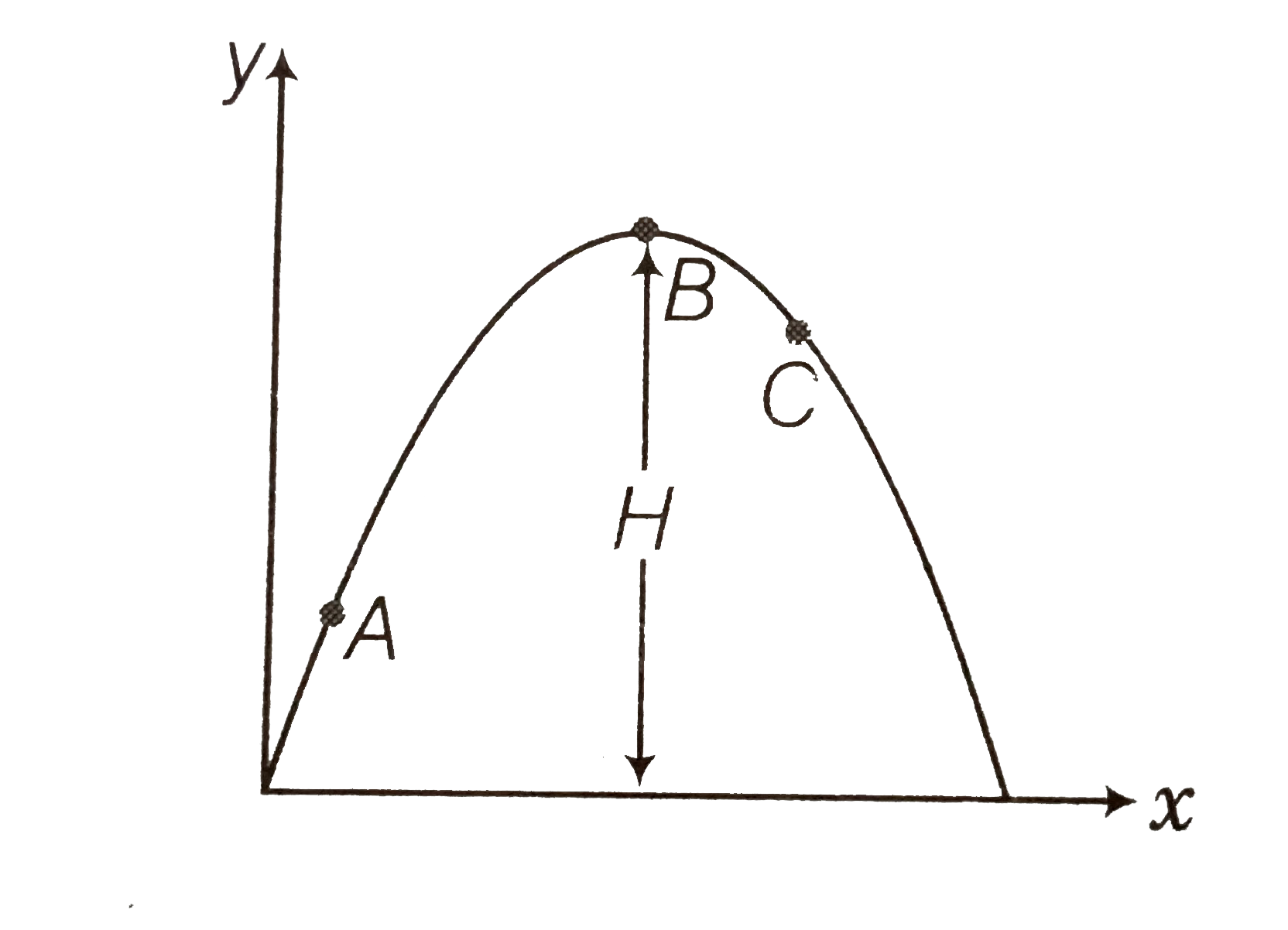 View Solution
View SolutionA particle moves along X-axis in such a way that its coordinate X varies with time t according to the equation x=(2−5t+6t2)m. The initial velocity of the particle is
View Solution

