A point is selected at random from the interior of a circle. The probability that the point is closer to the centre than the boundary of the circle is

$\frac{3}{4}$

$\frac{1}{2}$

$\frac{1}{4}$

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

Answer

Step by step video & text solution for A point is selected at random from the interior of a circle. The probability that the point is closer to the centre than the boundary of the circle is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS PROBABILITY

Topper's Solved these Questions

Knowledge Check

A point is selected randomly from the interior of a circle. The probability that the point is closer to the centre, then the boundary of circle is
A $\frac{3}{4}$
B $\frac{1}{4}$
C $\frac{1}{2}$
D $\frac{2}{3}$
A point is selected at random from inside a circle. The probability that the point is closer to the circumference of the circle than to its centre, is
A $\frac{2}{3}$
B $\frac{1}{3}$
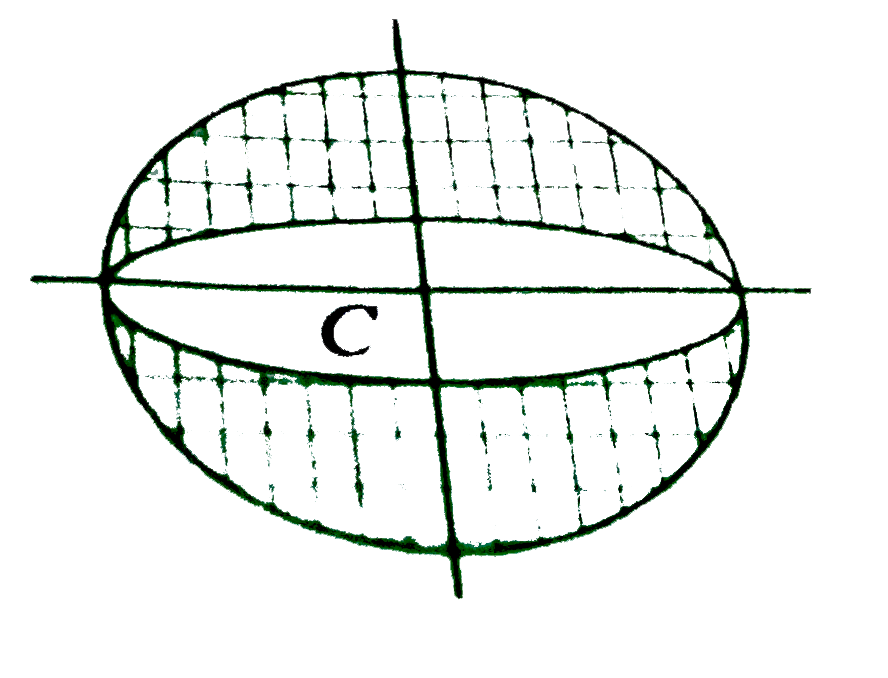
C $\frac{3}{4}$
D $\frac{1}{4}$
There are some experiment in which the outcomes cannot be identified discretely. For example, an ellipse of eccentricity $2 \sqrt{2} / 3$ is inscribed in a circle and a point within the circle is chosen at random. Now, we want to find the probability that this point lies outside the ellipse. Then, the point must lie in the shaded region shown in Figure. Let the radius of the circle be a and length of minor axis of the ellipse be 2b. Given that
$1 - \frac{b^{2}}{a^{2}} = \frac{8}{9} or \frac{b^{2}}{a^{2}} = \frac{1}{9}$
Then, the area of circle serves as sample space and area of the shaded region represents the area for favorable cases. Then, required probability is
$p = \frac{Area of shaded region}{Area of circle}$
$= \frac{π a^{2} - π a b}{π a^{2}} = 1 - \frac{b}{a} = 1 - \frac{1}{3} = \frac{2}{3}$
Now, answer the following questions.

A point is selected at random inside a circle. The probability that the point is closer to the center of the circle than to its circumference is
A $1 / 4$
B $1 / 2$
C $1 / 3$
D $1 / \sqrt{2}$

DISHA PUBLICATION-PROBABILITY-1-EXERCISE-2 : CONCEPT APPLICATOR

Home
Ask Doubt
Profile

A point is selected at random from the interior of a circle. The probability that the point is closer to the centre than the boundary of the circle is

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

A point is selected randomly from the interior of a circle. The probability that the point is closer to the centre, then the boundary of circle is

A point is selected at random from inside a circle. The probability that the point is closer to the circumference of the circle than to its centre, is

DISHA PUBLICATION-PROBABILITY-1-EXERCISE-2 : CONCEPT APPLICATOR