A printing company prints two types of magazines _A and 8. The company earns '10 and '15 on each magazine A and 8 respectively. These are processed on three machines I, II and Ill and total time in hours available per week on each machine is as follows.

The number of constraints is
3
4
5
6
The correct Answer is:C
Step by step video, text & image solution for A printing company prints two types of magazines _A and 8. The company earns '10 and '15 on each magazine A and 8 respectively. These are processed on three machines I, II and Ill and total time in hours available per week on each machine is as follows. The number of constraints is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - TARGET PUBLICATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - Competitive Thinking
35 Videos
- LINEAR PROGRAMMINGBOOK - TARGET PUBLICATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - Evaluation Test
11 Videos
- LINEAR PROGRAMMINGBOOK - TARGET PUBLICATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - Evaluation Test
11 Videos
- LINEBOOK - TARGET PUBLICATIONCHAPTER - LINEEXERCISE - Evaluation Test
1 Videos
- MATHEMATICAL LOGIC BOOK - TARGET PUBLICATIONCHAPTER - MATHEMATICAL LOGIC EXERCISE - EVALUATION TEST
14 Videos
Similar Questions
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each purpose and the time (in minutes) required for each toy on the machines is given below:
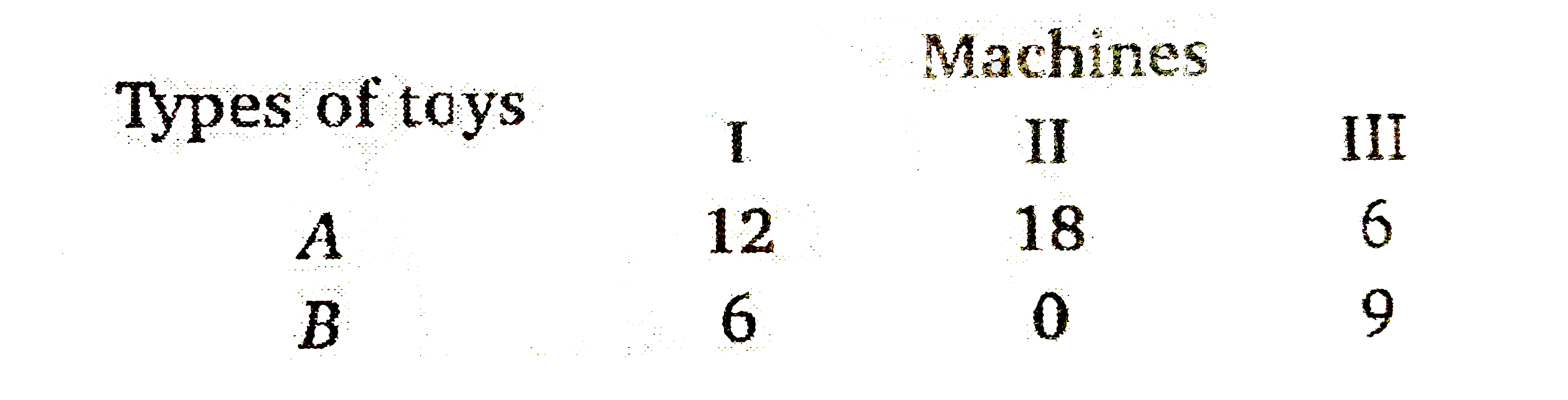
Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs. 7.50 and that on each toy of type B is Rs. 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
View SolutionA company manufactures two types of screws A and B. all the screws have to pass through a threading machine and a slotting machine. A box of type A screw requires 2min on the threading machine and 3 min on the slotting machine. A box of type B screw requires 8 min on the threading machine and 2 min on the slotting machine. In a week each machine is availbale for 60h. On selling these screws, the company gets a profit of 100 box on type A screw and 170 per box on type B screws. Formulate this problem as a LPP given that the objective is to maximise profit.
View Solution
Knowledge Check
A printing company prints two types of magzines A and B. The company earns Rs. 20 and Rs. 30 on each copy of magazines A and B respectively. The magazine A requires 2 hours on machine I, 4 hours on Machine II and 2 hours machine III. Magazine B requires 3 hours on machine I, 5 hours on machine II and 3 hours on machine III. Machines I,II, III are available for 35, 50 and 70 hours per week respectively. Formulate the LPP to determine weekly production of magazines A and B, so that the total profit is maximum
AMaximize z=20x+3y subject to 2x+3y≤35,4x+5y≤50,2x+3y≥70,x≥0,y≥0BMaximize z=20x+3y subject to 2x+3y≤35,4x+5y≤50,2x+3y≤70,x≥0,y≥0CMaximize z=20x+3y subject to 2x+3y≤35,4x+5y≥50,2x+3y≤70,x≥0,y≥0DMaximize z=20x+3y subject to 2x+3y≥35,4x+5y≤50,2x+3y≤70,x≥0,y≥0In a press, there are three types of printing machines, P, Q and R. Machine P can print 10,000 pages in 8 hours, machine Q can finish the same task in 10 hours and machine R can finish the same task in 15 hours. All the three machines start the work at 9:00 a. m. Machine P breaks down at 11:00 a.m. and machines Q and R finish the task. The approximate time of completion of the job is :
A2:05 p.m.B2:30 p.m.C1:50 p.m.D1:30 p.m.A tailor stiches trousers and shirts and each piece is completed by two machine I and II. To complete each trousers, machines I and II must work 3/2 hours and 2 hours respectively, and to complete each shirt, machines I and II must work 2 hours and 1 hours respectively Machine I may not operate for more than 12 hours ped day and machine II not more than 11 hours per day. If the profit on each trouser and each shirt is Rs. 150 and Rs. 100 repectively, then the maximum profit is _______
ARs. 900BRs. 500CRs. 375DRs. 600
A furniture form manufactures chairs and tables, each requiring the use of three machines A, B and C. Production of one chair requires 2 hours on machine A, 1 hour on machine B, and 1 hour on machine C. Each table requires 1 hour each on machines A and B and 3 hours on machine C. Profit realized by selling one chair is Rs. 30 while for a table the figure is Rs. 60. The total time available per week on machine A is 70 hours, on machine B is 40 hours, and on machine C is 90 hours. How many chairs and table should be made per week so as to maximize profit? Develop a mathematical formulation.
View SolutionA company manufactures two types of toys A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. He earns a profit of Rs.50 each on type A and Rs.60 each on type. B. How many toys of each type should the company manufacture in a day to maximize the profit ?
View SolutionA manufacturer makes two types of toys A and B.Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:

The machine I, II and III are available for a maximum of 3 hours, 2 hours and 2 hours 30 minutes respectively.The profit on each toy of type A is ₹ 50 and that of type B is ₹ 60.Formulate the above problem as a LPP and solve graphically to maximize profit.
View SolutionIn a small scale industry, a manufacturer produces two types of book cases. The first type of book case requires 3 hours on machine A and 2 hours on machine B for completion whereas the second type of book case requires 3 hours on machine A and 3 hours on machine B. The machines A and B respectively run for at the most 18 hours and 14 hours per day. He earns a profit of 30 on each type of case of first type and 40 on each book case of second type. How many book cases of each type should he manufacture so as to have maximum profit. Make it an LPP and solve it graphically.
View SolutionA manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the tune (in minutes) required for each toy on the machines is given below:Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs 7.50 and that on each toy of type B is Rs 5. show that 15 toys of type A and 30 of the B should be manufactured m a day to get maximum profit.
View Solution
