A random variable X as the following probability distribution: xi:−2−10123 pi:0.1k0.22k0.3k Find (i) Find the value of k. (ii) Calculate the mean ofX. Calculate the variance of X.
To solve the problem step by step, we will follow the instructions given in the question.
Step 1: Find the value of k
We know that the sum of all probabilities must equal 1. Therefore, we can write the equation:
\(
0.1 + k + 0.2 + 2k + 0.3 + k = 1
\)
Now, let's combine like terms:
\(
0.1 + 0.2 + 0.3 + k + 2k + k = 1
\)
This simplifies to:
\(
0.6 + 4k = 1
\)
Now, we can isolate k:
\(
4k = 1 - 0.6
\)
\(
4k = 0.4
\)
\(
k = \frac{0.4}{4} = 0.1
\)
Step 2: Calculate the mean of X
Now that we have the value of k, we can substitute it back into the probability distribution:
- \(p_i\) values become:
- \(p(-2) = 0.1\)
- \(p(-1) = 0.1\)
- \(p(0) = 0.2\)
- \(p(1) = 0.2\)
- \(p(2) = 0.3\)
- \(p(3) = 0.1\)
The mean \(E(X)\) is calculated using the formula:
\(
E(X) = \sum (x_i \cdot p_i)
\)
Calculating each term:
\(
E(X) = (-2 \cdot 0.1) + (-1 \cdot 0.1) + (0 \cdot 0.2) + (1 \cdot 0.2) + (2 \cdot 0.3) + (3 \cdot 0.1)
\)
Calculating each product:
\(
E(X) = -0.2 - 0.1 + 0 + 0.2 + 0.6 + 0.3
\)
Now, summing these values:
\(
E(X) = -0.2 - 0.1 + 0.2 + 0.6 + 0.3 = 0.8
\)
Step 3: Calculate the variance of X
The variance \(Var(X)\) is calculated using the formula:
\(
Var(X) = E(X^2) - (E(X))^2
\)
First, we need to calculate \(E(X^2)\):
\(
E(X^2) = \sum (x_i^2 \cdot p_i)
\)
Calculating each term:
\(
E(X^2) = (-2)^2 \cdot 0.1 + (-1)^2 \cdot 0.1 + (0)^2 \cdot 0.2 + (1)^2 \cdot 0.2 + (2)^2 \cdot 0.3 + (3)^2 \cdot 0.1
\)
Calculating each product:
\(
E(X^2) = 4 \cdot 0.1 + 1 \cdot 0.1 + 0 \cdot 0.2 + 1 \cdot 0.2 + 4 \cdot 0.3 + 9 \cdot 0.1
\)
Calculating these values:
\(
E(X^2) = 0.4 + 0.1 + 0 + 0.2 + 1.2 + 0.9
\)
Summing these values:
\(
E(X^2) = 0.4 + 0.1 + 0.2 + 1.2 + 0.9 = 2.8
\)
Now we can calculate the variance:
\(
Var(X) = E(X^2) - (E(X))^2
\)
Substituting the values we found:
\(
Var(X) = 2.8 - (0.8)^2
\)
\(
Var(X) = 2.8 - 0.64
\)
\(
Var(X) = 2.16
\)
Final Answers:
(i) The value of \(k\) is \(0.1\).
(ii) The mean of \(X\) is \(0.8\).
(iii) The variance of \(X\) is \(2.16\).
0.1 + k + 0.2 + 2k + 0.3 + k = 1
\)
0.1 + 0.2 + 0.3 + k + 2k + k = 1
\)
0.6 + 4k = 1
\)
4k = 1 - 0.6
\)
\(
4k = 0.4
\)
\(
k = \frac{0.4}{4} = 0.1
\)
- \(p(-2) = 0.1\)
- \(p(-1) = 0.1\)
- \(p(0) = 0.2\)
- \(p(1) = 0.2\)
- \(p(2) = 0.3\)
- \(p(3) = 0.1\)
E(X) = \sum (x_i \cdot p_i)
\)
E(X) = (-2 \cdot 0.1) + (-1 \cdot 0.1) + (0 \cdot 0.2) + (1 \cdot 0.2) + (2 \cdot 0.3) + (3 \cdot 0.1)
\)
E(X) = -0.2 - 0.1 + 0 + 0.2 + 0.6 + 0.3
\)
E(X) = -0.2 - 0.1 + 0.2 + 0.6 + 0.3 = 0.8
\)
Var(X) = E(X^2) - (E(X))^2
\)
E(X^2) = \sum (x_i^2 \cdot p_i)
\)
E(X^2) = (-2)^2 \cdot 0.1 + (-1)^2 \cdot 0.1 + (0)^2 \cdot 0.2 + (1)^2 \cdot 0.2 + (2)^2 \cdot 0.3 + (3)^2 \cdot 0.1
\)
E(X^2) = 4 \cdot 0.1 + 1 \cdot 0.1 + 0 \cdot 0.2 + 1 \cdot 0.2 + 4 \cdot 0.3 + 9 \cdot 0.1
\)
E(X^2) = 0.4 + 0.1 + 0 + 0.2 + 1.2 + 0.9
\)
E(X^2) = 0.4 + 0.1 + 0.2 + 1.2 + 0.9 = 2.8
\)
Var(X) = E(X^2) - (E(X))^2
\)
Var(X) = 2.8 - (0.8)^2
\)
\(
Var(X) = 2.8 - 0.64
\)
\(
Var(X) = 2.16
\)
(i) The value of \(k\) is \(0.1\).
(ii) The mean of \(X\) is \(0.8\).
(iii) The variance of \(X\) is \(2.16\).
Topper's Solved these Questions
Similar Questions
A random variable 'X' has the following probability distribution :

The values of k is
View SolutionA random variable X has the following probability distribution:
X: −2 −1 0 1 2 3
P(X):0.1 k 0.2 2k 0.3 k , find value of k
View SolutionA random varibale X has the following probability distribution.
X:12345P(X):00.10.20.30.4
Find the mean.
View SolutionA discrete random variable X has the probability distribution given below: X:0.511.52 P(X):kk22k2k Find the value of k. (ii) Determine the mean of the distribution.
View SolutionA random variable X has the following probability distribution: X=xi: 1 2 3 4 P(X=xi): k 2k 3k 4k Write the value of P(X≥3) .
View SolutionA random variable X has the following probability distribution:
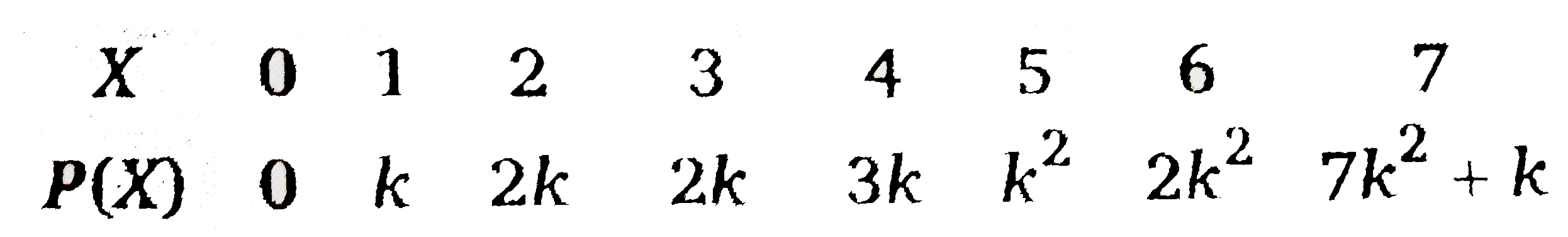
Determine :
(i) k
(ii) P(X<3)
(iii) P(X>6)
(iv) P(0<X<3)
View SolutionA random variable X has the following distribution
X=x1:−2−10123P(X=x1):0.1k0.22k0.3k
The value of k and its mean and variance are
View SolutionFind the mean and standard deviation of the following probability distribution: xi:2 3 4 pi:0.2 0.5 0.3
View SolutionFind the mean and variance for the following probability distribution: ∣∣∣xi1234pi0.40.30.20.1∣∣∣
View SolutionA discrete random variable X has the probability distribution as given below
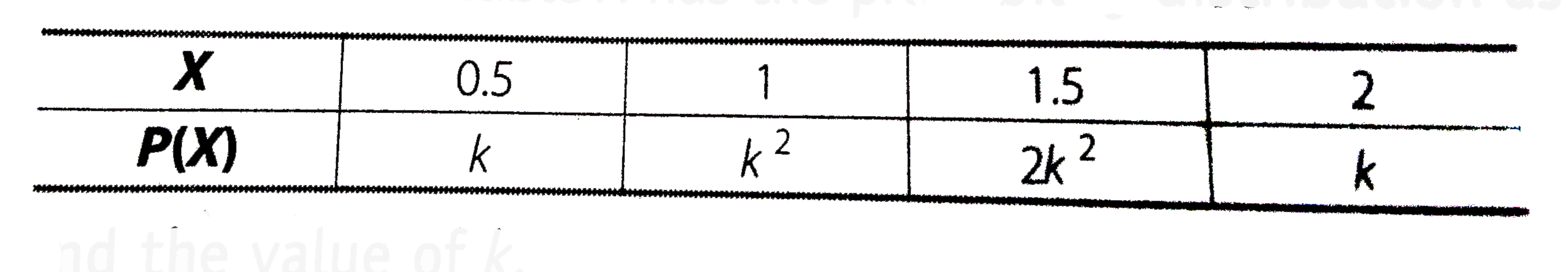
(i) Find the value of k.
(ii) Determine the mean of the distribution.
View Solution
