A random variable X has the following probability distribution: Values of X:0 1 2 3 4 5 6 7 8 P(x):a 3a 5a 7a 9a 11a 13a 15a 17a Determine: (i). The value of a (ii) P(X<3), P(X≥3), P(0<X<5)
To solve the given problem step by step, we will follow these steps:
Step 1: Find the value of a
We know that the sum of all probabilities in a probability distribution must equal 1.
The probabilities given are:
- \( P(X=0) = a \)
- \( P(X=1) = 3a \)
- \( P(X=2) = 5a \)
- \( P(X=3) = 7a \)
- \( P(X=4) = 9a \)
- \( P(X=5) = 11a \)
- \( P(X=6) = 13a \)
- \( P(X=7) = 15a \)
- \( P(X=8) = 17a \)
Now, we can write the equation for the total probability:
\(
a + 3a + 5a + 7a + 9a + 11a + 13a + 15a + 17a = 1
\)
Combining like terms:
\(
(1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17)a = 1
\)
Calculating the sum:
\(
1 + 3 = 4 \\
4 + 5 = 9 \\
9 + 7 = 16 \\
16 + 9 = 25 \\
25 + 11 = 36 \\
36 + 13 = 49 \\
49 + 15 = 64 \\
64 + 17 = 81
\)
Thus, we have:
\(
81a = 1
\)
Now, solving for a:
\(
a = \frac{1}{81}
\)
Step 2: Calculate \( P(X < 3) \)
To find \( P(X < 3) \), we need to find the probabilities for \( X = 0, 1, \) and \( 2 \):
\(
P(X < 3) = P(X=0) + P(X=1) + P(X=2)
\)
Substituting the values:
\(
P(X < 3) = a + 3a + 5a = 1a + 3a + 5a = 9a
\)
Now substituting \( a = \frac{1}{81} \):
\(
P(X < 3) = 9 \left(\frac{1}{81}\right) = \frac{9}{81} = \frac{1}{9}
\)
Step 3: Calculate \( P(X \geq 3) \)
To find \( P(X \geq 3) \), we sum the probabilities for \( X = 3, 4, 5, 6, 7, \) and \( 8 \):
\(
P(X \geq 3) = P(X=3) + P(X=4) + P(X=5) + P(X=6) + P(X=7) + P(X=8)
\)
Substituting the values:
\(
P(X \geq 3) = 7a + 9a + 11a + 13a + 15a + 17a = (7 + 9 + 11 + 13 + 15 + 17)a
\)
Calculating the sum:
\(
7 + 9 = 16 \\
16 + 11 = 27 \\
27 + 13 = 40 \\
40 + 15 = 55 \\
55 + 17 = 72
\)
Thus:
\(
P(X \geq 3) = 72a
\)
Substituting \( a = \frac{1}{81} \):
\(
P(X \geq 3) = 72 \left(\frac{1}{81}\right) = \frac{72}{81} = \frac{8}{9}
\)
Step 4: Calculate \( P(0 < X < 5) \)
To find \( P(0 < X < 5) \), we need to find the probabilities for \( X = 1, 2, 3, \) and \( 4 \):
\(
P(0 < X < 5) = P(X=1) + P(X=2) + P(X=3) + P(X=4)
\)
Substituting the values:
\(
P(0 < X < 5) = 3a + 5a + 7a + 9a = (3 + 5 + 7 + 9)a
\)
Calculating the sum:
\(
3 + 5 = 8 \\
8 + 7 = 15 \\
15 + 9 = 24
\)
Thus:
\(
P(0 < X < 5) = 24a
\)
Substituting \( a = \frac{1}{81} \):
\(
P(0 < X < 5) = 24 \left(\frac{1}{81}\right) = \frac{24}{81} = \frac{8}{27}
\)
Summary of Results
1. \( a = \frac{1}{81} \)
2. \( P(X < 3) = \frac{1}{9} \)
3. \( P(X \geq 3) = \frac{8}{9} \)
4. \( P(0 < X < 5) = \frac{8}{27} \)
We know that the sum of all probabilities in a probability distribution must equal 1.
- \( P(X=0) = a \)
- \( P(X=1) = 3a \)
- \( P(X=2) = 5a \)
- \( P(X=3) = 7a \)
- \( P(X=4) = 9a \)
- \( P(X=5) = 11a \)
- \( P(X=6) = 13a \)
- \( P(X=7) = 15a \)
- \( P(X=8) = 17a \)
\(
a + 3a + 5a + 7a + 9a + 11a + 13a + 15a + 17a = 1
\)
\(
(1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17)a = 1
\)
\(
1 + 3 = 4 \\
4 + 5 = 9 \\
9 + 7 = 16 \\
16 + 9 = 25 \\
25 + 11 = 36 \\
36 + 13 = 49 \\
49 + 15 = 64 \\
64 + 17 = 81
\)
Thus, we have:
\(
81a = 1
\)
\(
a = \frac{1}{81}
\)
To find \( P(X < 3) \), we need to find the probabilities for \( X = 0, 1, \) and \( 2 \):
\(
P(X < 3) = P(X=0) + P(X=1) + P(X=2)
\)
Substituting the values:
\(
P(X < 3) = a + 3a + 5a = 1a + 3a + 5a = 9a
\)
Now substituting \( a = \frac{1}{81} \):
\(
P(X < 3) = 9 \left(\frac{1}{81}\right) = \frac{9}{81} = \frac{1}{9}
\)
To find \( P(X \geq 3) \), we sum the probabilities for \( X = 3, 4, 5, 6, 7, \) and \( 8 \):
\(
P(X \geq 3) = P(X=3) + P(X=4) + P(X=5) + P(X=6) + P(X=7) + P(X=8)
\)
Substituting the values:
\(
P(X \geq 3) = 7a + 9a + 11a + 13a + 15a + 17a = (7 + 9 + 11 + 13 + 15 + 17)a
\)
Calculating the sum:
\(
7 + 9 = 16 \\
16 + 11 = 27 \\
27 + 13 = 40 \\
40 + 15 = 55 \\
55 + 17 = 72
\)
Thus:
\(
P(X \geq 3) = 72a
\)
Substituting \( a = \frac{1}{81} \):
\(
P(X \geq 3) = 72 \left(\frac{1}{81}\right) = \frac{72}{81} = \frac{8}{9}
\)
To find \( P(0 < X < 5) \), we need to find the probabilities for \( X = 1, 2, 3, \) and \( 4 \):
\(
P(0 < X < 5) = P(X=1) + P(X=2) + P(X=3) + P(X=4)
\)
Substituting the values:
\(
P(0 < X < 5) = 3a + 5a + 7a + 9a = (3 + 5 + 7 + 9)a
\)
Calculating the sum:
\(
3 + 5 = 8 \\
8 + 7 = 15 \\
15 + 9 = 24
\)
Thus:
\(
P(0 < X < 5) = 24a
\)
Substituting \( a = \frac{1}{81} \):
\(
P(0 < X < 5) = 24 \left(\frac{1}{81}\right) = \frac{24}{81} = \frac{8}{27}
\)
1. \( a = \frac{1}{81} \)
2. \( P(X < 3) = \frac{1}{9} \)
3. \( P(X \geq 3) = \frac{8}{9} \)
4. \( P(0 < X < 5) = \frac{8}{27} \)
Topper's Solved these Questions
Similar Questions
A random variable X has the following probability distribution: Values of X:0 1 2 3 4 5 6 7 8 P(x):a 3a 5a 7a 9a 11a 13a 15a 17a Determine: The value of a
View SolutionA random variable 'X' has the following probability distribution :

The values of k is
View SolutionA random variable X has the following probability distribution :

determine the value of a
View SolutionA random variable X has the following probability distribution: X=xi: 1 2 3 4 P(X=xi): k 2k 3k 4k Write the value of P(X≥3) .
View SolutionA random variable has the following probability distribution:
X=xi: 0 1 2 3 4 5 6 7
P(X=xi):0 2p 2p 3p p2 2p2 7p2 2p
The value of p is
a. 110
b. −1
c. −110
d. 15
View SolutionA random, variable X has the following probability distribution: X: 0 1 2 3 4 5 6 7 P(X):0 k 2k 2k 3k k2 2k2 7k2+k Find each of the following: i. k ii. P(X<6) iii. P(X≥6) iv. P(0<X<5)
View SolutionA random variable X has the following distribution .

The value of k and P(X<4) are equal to
View SolutionA random variable X has the following probability distribution:
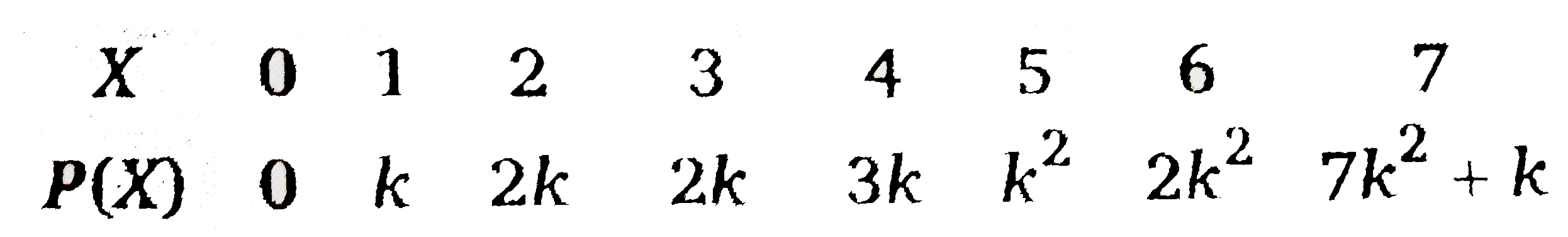
Determine :
(i) k
(ii) P(X<3)
(iii) P(X>6)
(iv) P(0<X<3)
View SolutionA discrete random variable X has the probability distribution given below: X: 0.5 1 1.5 2 P(X): k k2 2k2 k then, Find the value of k.
View SolutionA random variable X has the following probability distribution: X: 0 1 2 3 4 5 6 7 , P (X): 0 K 2K 2K 3K K2 2K2 7K2+K Determine: (i) K (ii) P(X<3) (iii) P(X > 6) (iv) P (0 < X < 3)
View Solution
