A discrete random variable X has the probability distribution given below: X: 0.5 1 1.5 2 P(X): k k2 2k2 k then, Find the value of k.
To find the value of k in the given probability distribution of the discrete random variable X, we follow these steps:
Step 1: Write down the given probability distribution.
We have:
- X:0.5,1,1.5,2
- P(X):k,k2,2k2,k
Step 2: Set up the equation for the sum of probabilities.
The sum of all probabilities must equal 1. Therefore, we can write the equation:
k+k2+2k2+k=1
Step 3: Combine like terms.
Combine the terms on the left side:
k+(k2+2k2)+k=1⟹k+3k2=1
Step 4: Rearrange the equation.
Rearranging gives us:
3k2+k−1=0
Step 5: Solve the quadratic equation.
We can use the quadratic formula k=−b±√b2−4ac2a, where a=3, b=1, and c=−1:
k=−1±√12−4⋅3⋅(−1)2⋅3
k=−1±√1+126
k=−1±√136
Step 6: Calculate the possible values of k.
Calculating the two possible values:
1. k=−1+√136
2. k=−1−√136
Step 7: Determine valid probabilities.
Since k must be a non-negative probability, we discard the negative solution:
k=−1+√136
Step 8: Approximate the value of k.
Calculating √13≈3.605:
k≈−1+3.6056≈2.6056≈0.434
Conclusion:
Thus, the value of k is approximately 0.434.
---
We have:
- X:0.5,1,1.5,2
- P(X):k,k2,2k2,k
The sum of all probabilities must equal 1. Therefore, we can write the equation:
k+k2+2k2+k=1
Combine the terms on the left side:
k+(k2+2k2)+k=1⟹k+3k2=1
Rearranging gives us:
3k2+k−1=0
We can use the quadratic formula k=−b±√b2−4ac2a, where a=3, b=1, and c=−1:
k=−1±√12−4⋅3⋅(−1)2⋅3
k=−1±√1+126
k=−1±√136
Calculating the two possible values:
1. k=−1+√136
2. k=−1−√136
Since k must be a non-negative probability, we discard the negative solution:
k=−1+√136
Calculating √13≈3.605:
k≈−1+3.6056≈2.6056≈0.434
Thus, the value of k is approximately 0.434.
Topper's Solved these Questions
Similar Questions
A random variable X has the following probability distribution: X=xi: 1 2 3 4 P(X=xi): k 2k 3k 4k Write the value of P(X≥3) .
View SolutionA random variable X has the following probability distribution:
X: −2 −1 0 1 2 3
P(X):0.1 k 0.2 2k 0.3 k , find value of k
View SolutionA discrete random variable X has the probability distribution given below: X:0.511.52 P(X):kk22k2k Find the value of k. (ii) Determine the mean of the distribution.
View SolutionA random variable 'X' has the following probability distribution :

The values of k is
View SolutionIf X is a random variable with probability distribution as given below: X=xi: 0 1 2 3 P(X=xi):k 3k 3k k The value of k and its variance are (A) 18,2227 (B) 18,2327 (C) 18,2427 (D) 18,34
View SolutionA random, variable X has the following probability distribution: X: 0 1 2 3 4 5 6 7 P(X):0 k 2k 2k 3k k2 2k2 7k2+k Find each of the following: i. k ii. P(X<6) iii. P(X≥6) iv. P(0<X<5)
View SolutionIf the probability distribution of a random variable X is given by X=xi: 1 2 3 4 P(X=xi): 2k 4k 3k k Write the value of k .
View SolutionThe probability distribution of a discrete random variable X is given below: X: 2 3 4 5 P(X):5k 7k 9k 11k The value of E(X) is
View SolutionA discrete random variable X has the probability distribution as given below
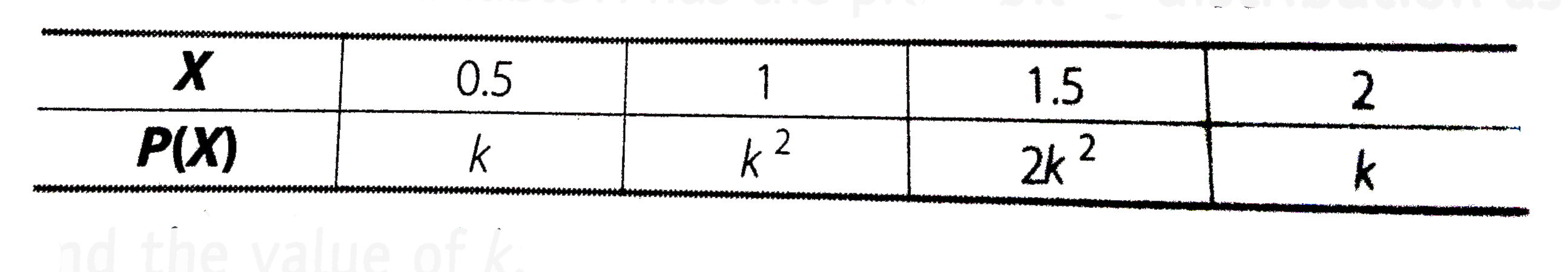
(i) Find the value of k.
(ii) Determine the mean of the distribution.
View SolutionA discrete random variable X has the probability distribution as given below
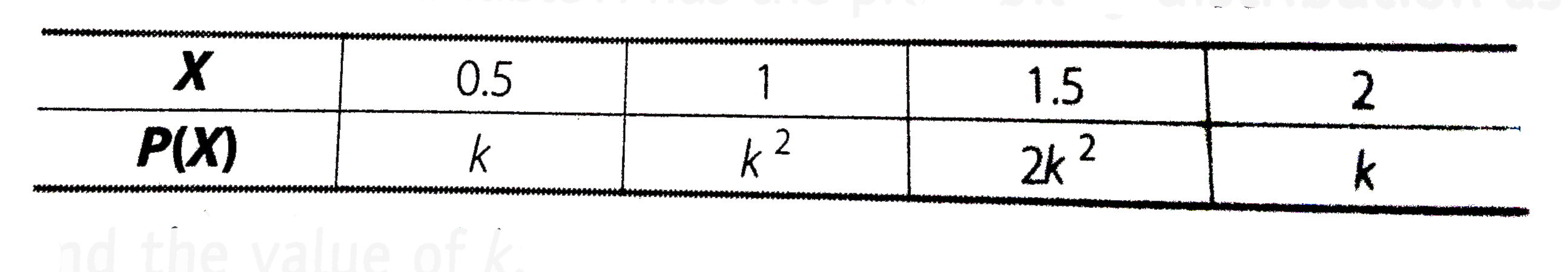
(i) Find the value of k.
(ii) Determine the mean of the distribution.
View Solution
