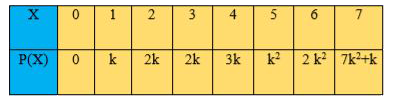
A random, variable X has the following probability distribution: X: 0 1 2 3 4 5 6 7 P(X):0 k 2k 2k 3k k2 2k2 7k2+k Find each of the following: i. k ii. P(X<6) iii. P(X≥6) iv. P(0<X<5)
To solve the problem step-by-step, we will follow the instructions given in the video transcript and derive the answers systematically.
Step 1: Find the value of k
We know that the sum of all probabilities in a probability distribution must equal 1. The probabilities given in terms of k are:
- \( P(X=0) = 0 \)
- \( P(X=1) = k \)
- \( P(X=2) = 2k \)
- \( P(X=3) = 2k \)
- \( P(X=4) = 3k \)
- \( P(X=5) = k^2 \)
- \( P(X=6) = 2k^2 \)
- \( P(X=7) = 7k^2 + k \)
Now, summing these probabilities:
\(
0 + k + 2k + 2k + 3k + k^2 + 2k^2 + (7k^2 + k) = 1
\)
Combining like terms:
\(
(0 + k + 2k + 2k + 3k + k + 7k^2 + 2k^2) = 1
\)
This simplifies to:
\(
9k + 10k^2 = 1
\)
Rearranging gives us:
\(
10k^2 + 9k - 1 = 0
\)
Now, we can solve this quadratic equation using the quadratic formula \( k = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \):
Here, \( a = 10, b = 9, c = -1 \):
\(
k = \frac{-9 \pm \sqrt{9^2 - 4 \cdot 10 \cdot (-1)}}{2 \cdot 10}
\)
\(
k = \frac{-9 \pm \sqrt{81 + 40}}{20}
\)
\(
k = \frac{-9 \pm \sqrt{121}}{20}
\)
\(
k = \frac{-9 \pm 11}{20}
\)
Calculating the two possible values:
1. \( k = \frac{2}{20} = \frac{1}{10} \)
2. \( k = \frac{-20}{20} = -1 \) (not valid since probabilities cannot be negative)
Thus, we have:
\(
k = \frac{1}{10}
\)
Step 2: Find \( P(X < 6) \)
To find \( P(X < 6) \), we need to sum the probabilities for \( X = 0, 1, 2, 3, 4, 5 \):
\(
P(X < 6) = P(X=0) + P(X=1) + P(X=2) + P(X=3) + P(X=4) + P(X=5)
\)
Substituting the values:
\(
P(X < 6) = 0 + k + 2k + 2k + 3k + k^2
\)
\(
= 0 + \frac{1}{10} + 2 \cdot \frac{1}{10} + 2 \cdot \frac{1}{10} + 3 \cdot \frac{1}{10} + \left(\frac{1}{10}\right)^2
\)
\(
= 0 + \frac{1}{10} + \frac{2}{10} + \frac{2}{10} + \frac{3}{10} + \frac{1}{100}
\)
\(
= \frac{8}{10} + \frac{1}{100}
\)
Finding a common denominator (100):
\(
= \frac{80}{100} + \frac{1}{100} = \frac{81}{100}
\)
Step 3: Find \( P(X \geq 6) \)
To find \( P(X \geq 6) \):
\(
P(X \geq 6) = 1 - P(X < 6)
\)
\(
= 1 - \frac{81}{100} = \frac{19}{100}
\)
Step 4: Find \( P(0 < X < 5) \)
To find \( P(0 < X < 5) \), we need to sum the probabilities for \( X = 1, 2, 3, 4 \):
\(
P(0 < X < 5) = P(X=1) + P(X=2) + P(X=3) + P(X=4)
\)
\(
= k + 2k + 2k + 3k
\)
\(
= \frac{1}{10} + 2 \cdot \frac{1}{10} + 2 \cdot \frac{1}{10} + 3 \cdot \frac{1}{10}
\)
\(
= \frac{1 + 2 + 2 + 3}{10} = \frac{8}{10} = \frac{4}{5}
\)
Summary of Answers
i. \( k = \frac{1}{10} \)
ii. \( P(X < 6) = \frac{81}{100} \)
iii. \( P(X \geq 6) = \frac{19}{100} \)
iv. \( P(0 < X < 5) = \frac{4}{5} \)
- \( P(X=1) = k \)
- \( P(X=2) = 2k \)
- \( P(X=3) = 2k \)
- \( P(X=4) = 3k \)
- \( P(X=5) = k^2 \)
- \( P(X=6) = 2k^2 \)
- \( P(X=7) = 7k^2 + k \)
0 + k + 2k + 2k + 3k + k^2 + 2k^2 + (7k^2 + k) = 1
\)
(0 + k + 2k + 2k + 3k + k + 7k^2 + 2k^2) = 1
\)
9k + 10k^2 = 1
\)
10k^2 + 9k - 1 = 0
\)
k = \frac{-9 \pm \sqrt{9^2 - 4 \cdot 10 \cdot (-1)}}{2 \cdot 10}
\)
\(
k = \frac{-9 \pm \sqrt{81 + 40}}{20}
\)
\(
k = \frac{-9 \pm \sqrt{121}}{20}
\)
\(
k = \frac{-9 \pm 11}{20}
\)
2. \( k = \frac{-20}{20} = -1 \) (not valid since probabilities cannot be negative)
k = \frac{1}{10}
\)
P(X < 6) = P(X=0) + P(X=1) + P(X=2) + P(X=3) + P(X=4) + P(X=5)
\)
P(X < 6) = 0 + k + 2k + 2k + 3k + k^2
\)
\(
= 0 + \frac{1}{10} + 2 \cdot \frac{1}{10} + 2 \cdot \frac{1}{10} + 3 \cdot \frac{1}{10} + \left(\frac{1}{10}\right)^2
\)
\(
= 0 + \frac{1}{10} + \frac{2}{10} + \frac{2}{10} + \frac{3}{10} + \frac{1}{100}
\)
\(
= \frac{8}{10} + \frac{1}{100}
\)
Finding a common denominator (100):
= \frac{80}{100} + \frac{1}{100} = \frac{81}{100}
\)
P(X \geq 6) = 1 - P(X < 6)
\)
\(
= 1 - \frac{81}{100} = \frac{19}{100}
\)
P(0 < X < 5) = P(X=1) + P(X=2) + P(X=3) + P(X=4)
\)
\(
= k + 2k + 2k + 3k
\)
\(
= \frac{1}{10} + 2 \cdot \frac{1}{10} + 2 \cdot \frac{1}{10} + 3 \cdot \frac{1}{10}
\)
\(
= \frac{1 + 2 + 2 + 3}{10} = \frac{8}{10} = \frac{4}{5}
\)
Similar Questions
Knowledge Check
- Question 1 - Select One
A random variable X has following probability distribution
X=x123456P(X=x)K3K5K7K8KK
Then P(2≤X<5)= . . . .A35B725C2325D2425
A random variable X has the following probability distribution:Determine (i) k (ii) P(X<3)(iii) P(X>6) (iv) P(0<X<3)
View SolutionA random variable X has the following probability distribution: I 0 1 2 3 4 5 6 7 P (X) 0 K 2K 2K 3K K2 2K2 7K2+K Determine: (i) K (ii) P(X<3) (iii) P(X > 6) (iv) P (0 < X < 3)
View SolutionA random variable X has the following probability distribution: X=xi: 1 2 3 4 P(X=xi): k 2k 3k 4k Write the value of P(X≥3) .
View SolutionA random variable X has the following probability distribution: [X=x0123P(X=x)181214k]
View SolutionA random variable X as the following probability distribution: xi:−2−10123 pi:0.1k0.22k0.3k Find (i) Find the value of k. (ii) Calculate the mean ofX. Calculate the variance of X.
View SolutionThe probability distribution of X is as follows:
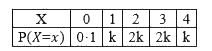
Find k and P [X<2].View SolutionA random variable 'X' has a probability distribution P(X) of the following form (k is constant):

then k = __________ .View Solution