A random, variable X has the following probability distribution: X: 0 1 2 3 4 5 6 7 P(X):0 k 2k 2k 3k k2 2k2 7k2+k Find each of the following: k ii. P(X<6) iii. P(∣X≥6) iv. P(0<x,5)
19100
81100
9100
91100
The correct Answer is:A
Since the sum of the probabilities in a probability distribution is always unity.
∴P(X=0)+P(X=1)+.....+P(X=7)=1
⇒0+k+2k+2k+3k+k2+2k2+7k2+k=1
⇒10k2+9k−1=0
⇒(10k−1)(k+1)=0
⇒10k−1=0 [∵k≥0∴k+1≠0]
⇒k=110
Now,
P(X≥6)=P(X=6)+P(X=7)=2k2+7k2+k=9k2+k=19100 (k=1/10]
Topper's Solved these Questions
- DISCRETE PROBABILITY DISTRIBUTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Section I - Solved Mcqs
39 Videos
- DISCRETE PROBABILITY DISTRIBUTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Section II - Assertion Reason Type
1 Videos
- DETERMINANTSBOOK - OBJECTIVE RD SHARMACHAPTER - DETERMINANTSEXERCISE - Chapter Test
30 Videos
- FUNCTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - FUNCTIONSEXERCISE - Chapter Test
30 Videos
Similar Questions
A random, variable X has the following probability distribution: X: 0 1 2 3 4 5 6 7 P(X):0 k 2k 2k 3k k2 2k2 7k2+k Find each of the following: i. k ii. P(X<6) iii. P(X≥6) iv. P(0<X<5)
View SolutionA random variable X has the following probability distribution: Values of X: −2 −1 0 1 2 3 P(X):0.1 k 0.2 2k 0.3 k
View Solution
Knowledge Check
A random variable X has following probability distribution
X=x123456P(X=x)K3K5K7K8KK
Then P(2≤X<5)= . . . .A35B725C2325D2425
A random variable X has the following probability distribution:Determine (i) k (ii) P(X<3)(iii) P(X>6) (iv) P(0<X<3)
View SolutionA random variable X has the following probability distribution: I 0 1 2 3 4 5 6 7 P (X) 0 K 2K 2K 3K K2 2K2 7K2+K Determine: (i) K (ii) P(X<3) (iii) P(X > 6) (iv) P (0 < X < 3)
View SolutionA random variable X has the following probability distribution: X=xi: 1 2 3 4 P(X=xi): k 2k 3k 4k Write the value of P(X≥3) .
View SolutionA random variable X has the following probability distribution: [X=x0123P(X=x)181214k]
View SolutionA random variable X as the following probability distribution: xi:−2−10123 pi:0.1k0.22k0.3k Find (i) Find the value of k. (ii) Calculate the mean ofX. Calculate the variance of X.
View SolutionThe probability distribution of X is as follows:
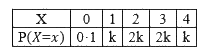
Find k and P [X<2].
View SolutionA random variable 'X' has a probability distribution P(X) of the following form (k is constant):

then k = __________ .
View Solution
