A ray of light comes along the line L = 0 and strikes the plane mirror kept along the plane P = 0 at B. A(2,1,6) is a point on the line L = 0 whose image about P = 0 is A'. It is given that L = 0 is x−23=y−14=z−65andP=0 is x+y−2z=3.
If L1=0 is the reflected ray, then its equation is Solution in Bengali
x+104=y−54=z+23
x+103=y+155=z+145
x+104=y+155=z+143
none of these
The correct Answer is:c
The equation of the reflected ray L1=0 is the line joining Q(x2,y2,z2)andB(−10,−15,−14).
x+1016=y+1520=z+1412
or x+104=y+155=z+143
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MATRIX-MATCH TYPE
5 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - INTEGER TYPE
10 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - REASONING TYPE
10 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
291 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)
4 Videos
Similar Questions
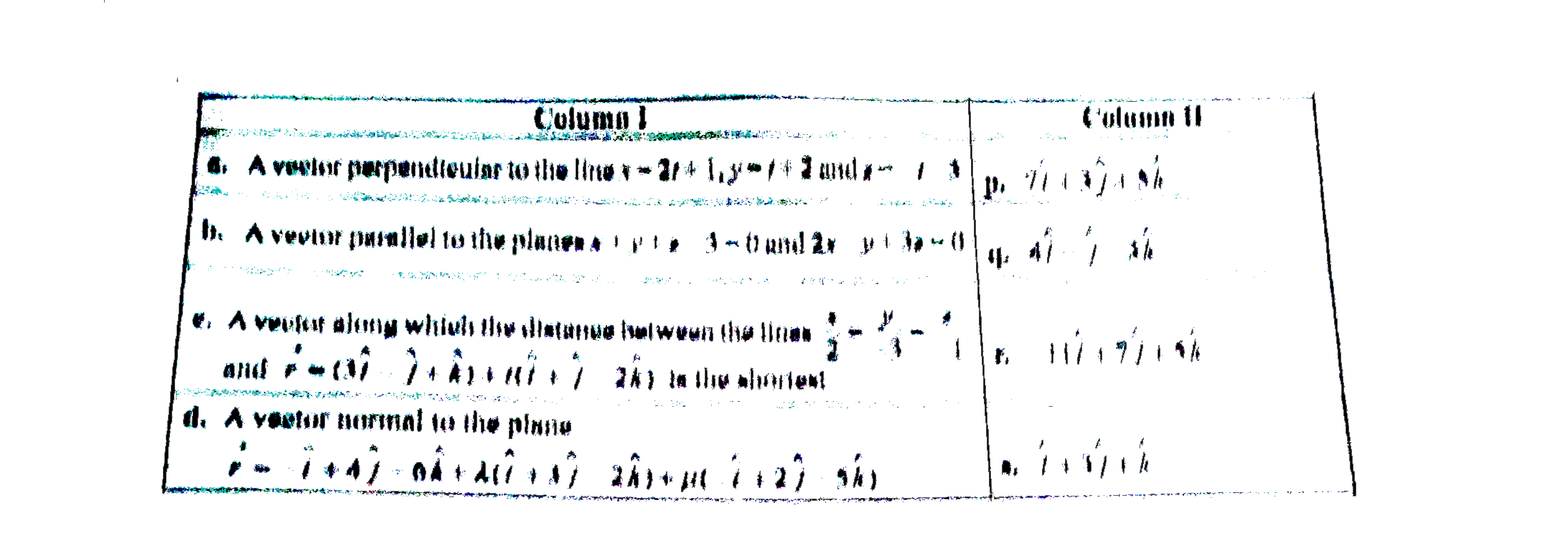
View SolutionFind the number of sphere of radius r touching the coordinate axes.
View SolutionStatement 1: Lines →r=ˆi+ˆj−ˆk+λ(3ˆi−ˆj)and→r=4ˆi−ˆk+μ(2ˆi+3ˆk) intersect. Statement 2: →b×→d=0 , then lines →r=→a+λ→band→r=→c+λ→d do not intersect.
View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
View SolutionA ray of light comes light comes along the line L = 0 and strikes the plane mirror kept along the plane P = 0 at B. A(2,1,6) is a point on the line L = 0 whose image about P = 0 is A'. It is given that L = 0 is x−23=y−14=z−65andP=0 is x+y−2z=3.
If L1=0 is the reflected ray, then its equation is
View SolutionLet image of the line x−13=y−35=z−42 in the plane 2x−y+z+3=0 be L. A plane 7x+By+Cz+3D=0 is such that if contains the line L and perpendicular to the plane 2x−y+z+3=0 then the value of B+C+D=
View Solutionयदि समतलों 2x−2y+3z−2=0,x−y+z+1=0, की परिच्छेदी रेखा L1 है तथा समतलों x+2y−z−3=0,3x−y+2z−1=0 की परिच्छेदी रेखा L2 है तो मूल बिंदू की दूरी उस समतल से जो रेखाओं L1 और L2 का अंतर्विष्ट करता है:
(i) 12√2 (ii) 1√2 (iii) 14√2 (iv) 13√2
View SolutionA ray of light comes light comes along the line L = 0 and strikes the plane mirror kept along the plane P = 0 at B. A(2,1,6) is a point on the line L = 0 whose image about P = 0 is A'. It is given that L = 0 is x−23=y−14=z−65andP=0 is x+y−2z=3.
If L1=0 is the reflected ray, then its equation is
View SolutionA ray of light coming along the line x−11=y−22=z−33 , strikes the plane mirror kept along the plane through points (2,1,1),(3,0,2)and(2,−1,−2) . Then the equation of reflected ray is:
View Solutionयदि समतलों 2x−2y+3z−2=0,x−y+z+1=0, की परिच्छेदी रेखा L1 है तथा समतलों x+2y−z−3=0,3x−y+2z−1=0 की परिच्छेदी रेखा L2 है तो मूल बिंदू की दूरी उस समतल से जो रेखाओं L1 और L2 का अंतर्विष्ट करता है:
(i) 12√2 (ii) 1√2 (iii) 14√2 (iv) 13√2
View Solutionएक प्रकाश की किरण रेखा L = 0 के अनुदिश आती है और B पर समतल P=0 के अनुदिश रखे समतल दर्पण से टकराती है बिन्दु A(2,1,6) रेखा L=0 पर स्थित है जिसका प्रतिबिम्ब P=0 के सापेक्ष A है, यह दिया जाता है कि L=0,x−23=y−14=z−65 है तथा P=0,x+y−2z=3 है।
A' के निर्देशांक हैं
View Solutionएक प्रकाश की किरण रेखा L = 0 के अनुदिश आती है और B पर समतल P=0 के अनुदिश रखे समतल दर्पण से टकराती है बिन्दु A(2,1,6) रेखा L=0 पर स्थित है जिसका प्रतिबिम्ब P=0 के सापेक्ष A है, यह दिया जाता है कि L=0,x−23=y−14=z−65 है तथा P=0,x+y−2z=3 है।
B के निर्देशांक हैं
View Solutionएक प्रकाश की किरण रेखा L = 0 के अनुदिश आती है और B पर समतल P=0 के अनुदिश रखे समतल दर्पण से टकराती है बिन्दु A(2,1,6) रेखा L=0 पर स्थित है जिसका प्रतिबिम्ब P=0 के सापेक्ष A है, यह दिया जाता है कि L=0,x−23=y−14=z−65 है तथा P=0,x+y−2z=3 है।
यदि L1=0 परिवर्तित किरण हो, तो इसका समीकरण है
View SolutionLet L1:x−11=y+12=z−22L2:x−2y−1=0λy−z+2π:2x+y−z=0
If the line L2 ies in the plane L3 then angle between the lines L1,L2
View SolutionIf P (2,3,1) is a point and L≡x−y−z−2=0 is a plane then
View Solution
