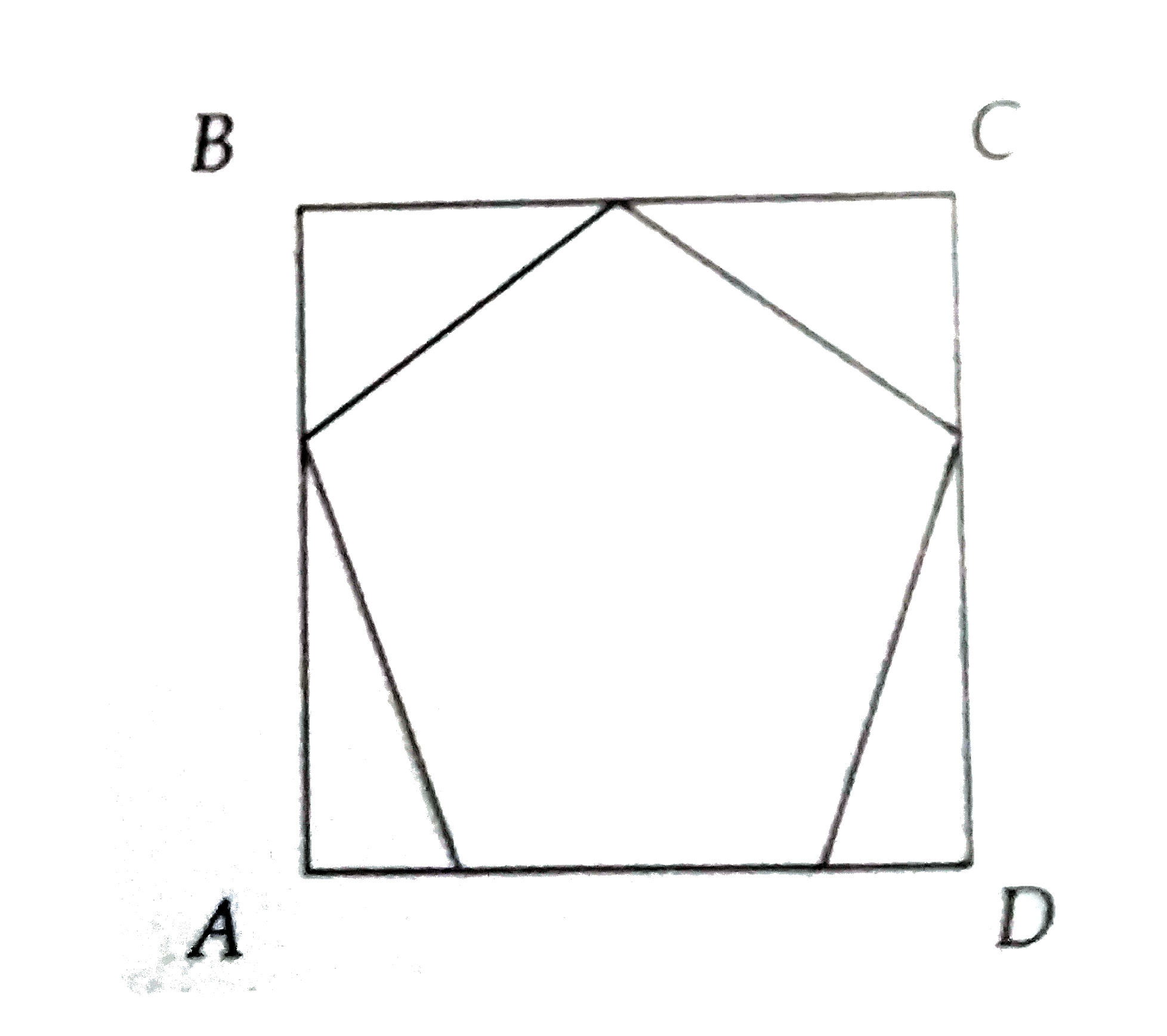
A regular pentagon with all of its vertices on the sides of a rectangle. If BC=14, what is the perimeter of the pentagon ?
0.31
0.62
0.77
0.80
The correct Answer is:C
The angles of the rectangle are right angles. To figure out the interior angles of the pentagon, use the formula for the degree measure of each interior angle of a regular polygon of n sides :
Interior angle =(n−2)180n
=(5−2)1805
=180
Lable all the angles you can :

The angles marked a∘ are equal and together with 108∘ add up to 180∘.
108+2a=180
2a=72
a=36
So the right triangle in the upper left looks like this :
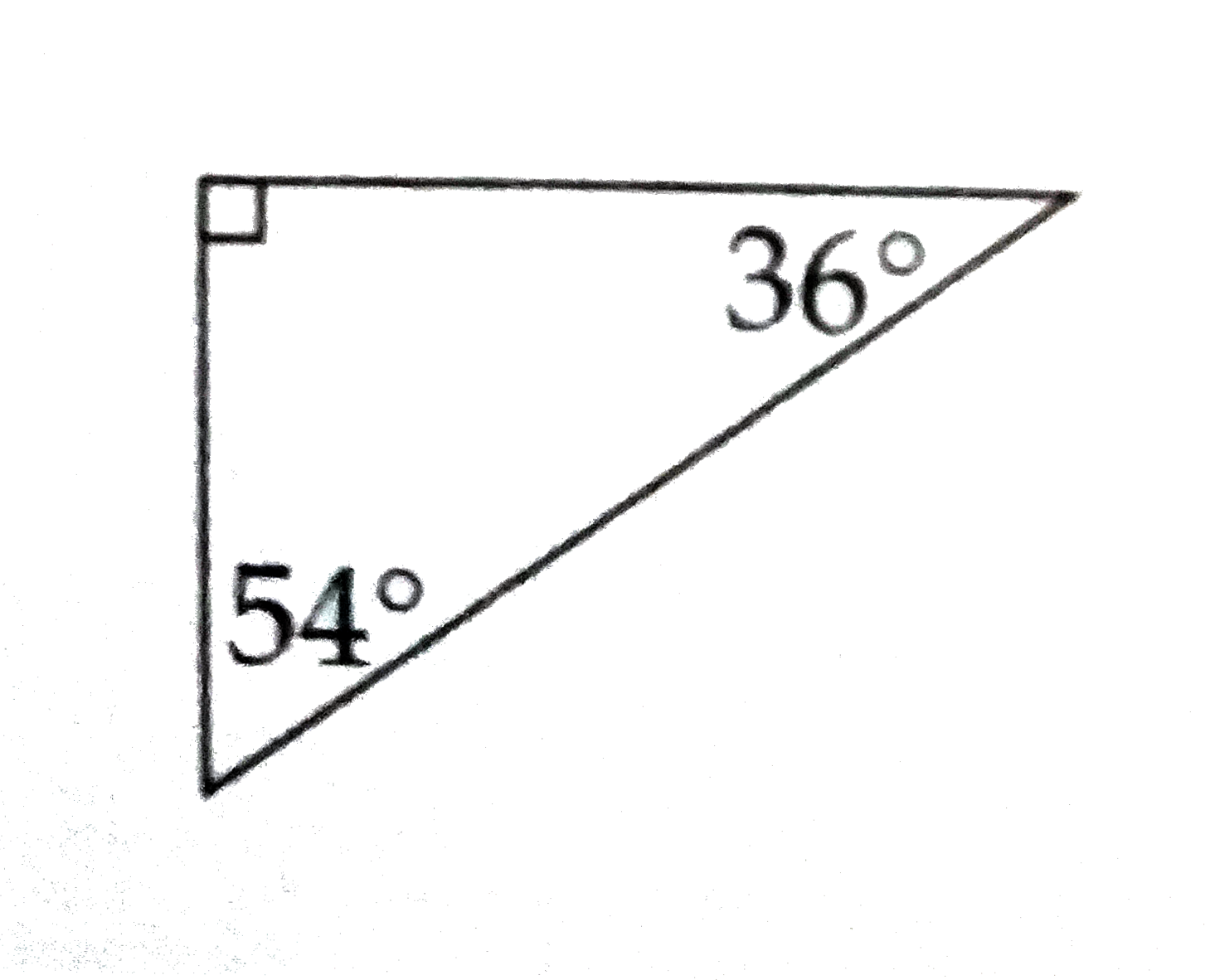
The leg on top (opposite the 54∘ angle) is half of BC, or 18. The hypotenuse of this right triangle is one side of the pentagon whose perimeter you are looking for, so call the hypotenuse x :

You have the leg that's opposite the 54∘ and you're looking for the hypotenuse, so use the sine :
sin54∘=18x
x=18sin54∘≈0.155
That's not the answer, however. That's just one side of the pentagon, and you want the perimeter, so multiply that side length by 5 :
Perimeter ≈5×0.155≈0.77
Similar Questions
Knowledge Check
What is the perimeter of a regular pentagon with a side of 3.5 cm ?
A17.5 cmB28 cmC15 cmD12.25 cmIf the side of a regular pentagon be 2 cm, find the circumference of the pentagon, in cm.
A1. 10cmB2. 15 cmC3. 20cmD4. 5 cm
A pentagon has three sides with length x, and two sides with the length 3x. If x is 23 of an inch, what is the perimeter of the pentagon?
View SolutionSymmetry of a regular pentagon.
View SolutionIf the sides of a regular pentagon are l, find the rule that gives the perimeter of the pentagon. Also, use rule to find the perimeter if the side of the pentagon is 7 cm.
View Solution8. Find the perimeter of the regular hexagon with each side measuring 8m (9).Find the side of a square whose perimeter is 20m( 10).The perimeter of a regular pentagon is 100 cm. How long is its each side?
View Solution8. Find the perimeter of the regular hexagon with each side measuring 8m (9).Find the side of a square whose perimeter is 20m( 10).The perimeter of a regular pentagon is 100 cm. How long is its each side?
View SolutionLines of symmetry of a regular pentagon
View Solution
