A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
The correct Answer is:π cm^3
To find the volume of the solid that consists of a cone standing on a hemisphere, we will follow these steps:
Step 1: Identify the dimensions
Given:
- Radius of the cone (r) = 1 cm
- Height of the cone (h) = 1 cm (since the height of the cone is equal to its radius)
- Radius of the hemisphere = 1 cm
Step 2: Calculate the volume of the cone
The formula for the volume of a cone is:
Vcone=13πr2h
Substituting the values:
Vcone=13π(1)2(1)=13π⋅1⋅1=13π
Step 3: Calculate the volume of the hemisphere
The formula for the volume of a hemisphere is:
Vhemisphere=23πr3
Substituting the value of the radius:
Vhemisphere=23π(1)3=23π⋅1=23π
Step 4: Calculate the total volume of the solid
The total volume of the solid is the sum of the volume of the cone and the volume of the hemisphere:
Vtotal=Vcone+Vhemisphere
Substituting the calculated volumes:
Vtotal=13π+23π=1+23π=33π=π
Step 5: State the final answer
The volume of the solid in terms of π is:
Volume=π cm3
Given:
- Radius of the cone (r) = 1 cm
- Height of the cone (h) = 1 cm (since the height of the cone is equal to its radius)
- Radius of the hemisphere = 1 cm
The formula for the volume of a cone is:
Vcone=13πr2h
Substituting the values:
Vcone=13π(1)2(1)=13π⋅1⋅1=13π
The formula for the volume of a hemisphere is:
Vhemisphere=23πr3
Substituting the value of the radius:
Vhemisphere=23π(1)3=23π⋅1=23π
The total volume of the solid is the sum of the volume of the cone and the volume of the hemisphere:
Vtotal=Vcone+Vhemisphere
Substituting the calculated volumes:
Vtotal=13π+23π=1+23π=33π=π
The volume of the solid in terms of π is:
Volume=π cm3
Topper's Solved these Questions
- SURFACE AREAS AND VOLUMESBOOK - NCERT ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Exercise 13.3
9 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERT ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Solved Examples
14 Videos
- STATISTICSBOOK - NCERT ENGLISHCHAPTER - STATISTICSEXERCISE - EXERCISE 14.1
9 Videos
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 6.1
3 Videos
Similar Questions
A solid is in the form of a cone standing on a hemi-sphere with both their radii being equal to 8 cm and the height of cone is equal to its radius. Find the volume of the solid in terms of pi .
View SolutionA solid is in the form of a cone standing on a hemisphere with both their radii being equal to 8 cm and the height of cone is equal to its radius . Find the volume of solid.
View SolutionA solid is in the shape of a cone surmounted on a hemi-sphere, the radius of each of them is being 3.5 cm and the total height of solid is 9.5 cm. Find the volume of the solid. (Use π=22/7 )
View SolutionA solid wooden toy is in the shape of a right circular cone mounted on a hemisphere. If the radius of the hemisphere is 4.2 cm and the total height of the toy is 10.2 cm, find the volume of the wooden toy.
View SolutionA solid wooden toy is in the shape of a right circular cone mounted on a hemisphere. If the radius of the hemisphere is 4.2 cm and the total height of the toy is 10.2 cm, find the volume of the wooden toy.
View SolutionThe height of a cone is 7 cm and its radius of base is 3 cm. Find its volume.
View SolutionA cone and a hemisphere have equal bases and equal volumes. The ratio of their heights is
View SolutionA solid is in the shape of a frustum of a cone. The diameters of the two circular ends are 60 cm and 36 cm and the height is 9 cm. Find the area of its whole surface and the volume.
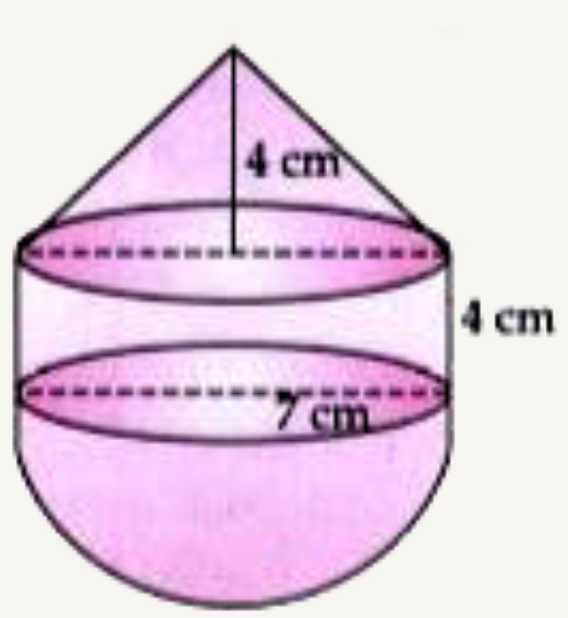
View SolutionThe following figure represents a solid consiting of right circular cylinder with a hemisphere at one end and a cone at the other. Their common radius is 7 cm. The height of the cylinder and cone are each of 4 cm. Find the volume of the solid.
View SolutionA cone and a hemisphere have equal bases and equal volumes. Find the ratio of their heights.
View Solution
