Selvis house has an overhead tank in the shape of a cylinder. This is filled by pumping water from a sump (an underground tank) which is in the shape of a cuboid. The sump has dimensions 1.57m×1.44m×95cm. The overhead tank has its radius
To solve the problem step by step, we will calculate the volume of both the overhead tank (cylinder) and the sump (cuboid), and then determine the height of the water left in the sump after filling the overhead tank.
Step 1: Calculate the volume of the overhead tank (cylinder)
The formula for the volume V of a cylinder is given by:
V=πr2h
Where:
- r = radius of the cylinder
- h = height of the cylinder
Given:
- Radius r=60cm=0.6m (converted to meters)
- Height h=95cm=0.95m
Substituting the values into the formula:
V=π(0.6)2(0.95)
V=3.14×0.36×0.95
V≈1.067m3
Step 2: Calculate the volume of the sump (cuboid)
The formula for the volume V of a cuboid is given by:
V=length×breadth×height
Given:
- Length = 1.57m
- Breadth = 1.44m
- Height = 0.95m
Substituting the values into the formula:
V=1.57×1.44×0.95
V≈2.157m3
Step 3: Calculate the volume of water left in the sump after filling the overhead tank
The volume of water left in the sump after filling the overhead tank is given by:
Volume left=Volume of sump−Volume of overhead tank
Substituting the volumes calculated:
Volume left=2.157−1.067
Volume left≈1.090m3
Step 4: Calculate the height of the water left in the sump
To find the height of the water left in the sump, we can use the formula for the volume of a cuboid:
Volume left=length×breadth×height left
Rearranging the formula to find the height left:
height left=Volume leftlength×breadth
Substituting the values:
height left=1.0901.57×1.44
height left=1.0902.2568
height left≈0.483mor48.3cm
Step 5: Compare the capacity of the overhead tank with that of the sump
The capacity of the overhead tank is approximately 1.067m3 and the capacity of the sump is approximately 2.157m3.
To compare:
Capacity ratio=Capacity of overhead tankCapacity of sump=1.0672.157≈0.495
This means the capacity of the overhead tank is about half of the capacity of the sump.
- r = radius of the cylinder
- h = height of the cylinder
- Radius r=60cm=0.6m (converted to meters)
- Height h=95cm=0.95m
V=3.14×0.36×0.95
V≈1.067m3
- Length = 1.57m
- Breadth = 1.44m
- Height = 0.95m
V≈2.157m3
Volume left≈1.090m3
height left=1.0902.2568
height left≈0.483mor48.3cm
Topper's Solved these Questions
- SURFACE AREAS AND VOLUMESBOOK - NCERT ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - EXERCISE 13.2
8 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERT ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Exercise 13.3
9 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERT ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - EXERCISE 13.5
7 Videos
- STATISTICSBOOK - NCERT ENGLISHCHAPTER - STATISTICSEXERCISE - EXERCISE 14.1
9 Videos
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 6.1
3 Videos
Similar Questions
A overhead tank of capacity 1000 liter has to be filled in 12 hour using water pump. Tank is kept at a height 10 m above ground and water level is 10 m below ground. The opening of inlet pipe inside tank is 1.11cm2. Assuming the efficiency of motor to be 60%, the electric power used is (Neglect viscosity)
View SolutionT=R2r2√2hg
Suppose an open cylindrical tank has a round drain with radius t in the bottom of the tank. When the tank is filled with water to a depth of h centimeters, the time it takes for all the water to drain from the tank is given by the formula above, where R is the radius of the tank (in centimeters) and g=980cm/s2 is the acceleration due to gravity. Suppose such a tank has a radius of 2 meters and is filled to a depth of 4 meters. About how many minutes does it take to empty the tank if the drain has a radius of 5 centimeters? (1 meter=100 centimeter).
View Solution
Knowledge Check
A rectangular fish tank fish has a base 2 feet wide and 2 feet long. When the tank is partially filled with water, a solid cube with an edge length of 1 foot is placed in the tank. If no overflow of water from the tank is assumed, by how many inches will be level of the water in the tank rise when the cube becomes completely submerged?
A16B12C2D3
In the adjoining line diagram, a birds is shwon having its one eye, two legs and one tail in shaded portions. Head and lower part are formed with two quarter circles A and B with diameters 10 cm each and two semicircles C and D with diameters 4 cm each. An eye has a radius 0.5 cm. Each leg is in the shape of equilateral Δ with sides 1 cm each and a tail is a trapezium with parallel sides 1 cm and 3 cm and the distance between these sides is 1.5 cm. Find the area covered by this bird. (Take π=3.14,√3=1.732)
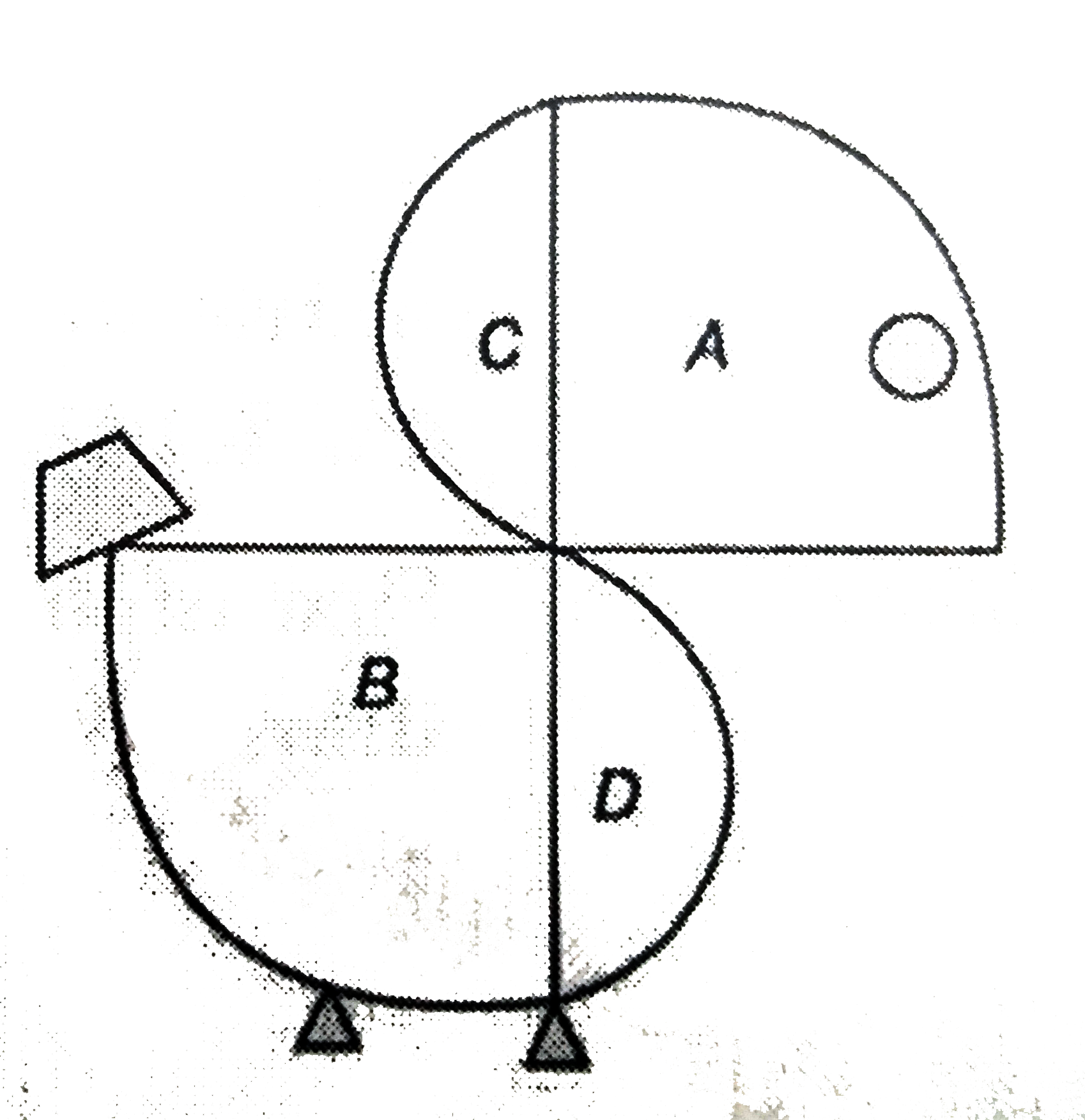
View SolutionA tank, with a square base of area 1.0m2 is divided by a vertical partition has a small hinged door of aren 20cm2. The tank is filled with water in one compartment, and an acid (of relative density 1.7) in the other, both to the height of 4.0 m. Compute the force necessary to keep the door closed
View SolutionA particle lies on the bottom of a tank T filled with water upto s height of 90cm. The medium above the surface of water is of R.I=1.2 above which there is mirror M. Beyond the mirror M the region contains air (μ=1). The distance of the image formed by the mirrro after reflection of the rays coming from P is ____ cm (w.r.t mirror).
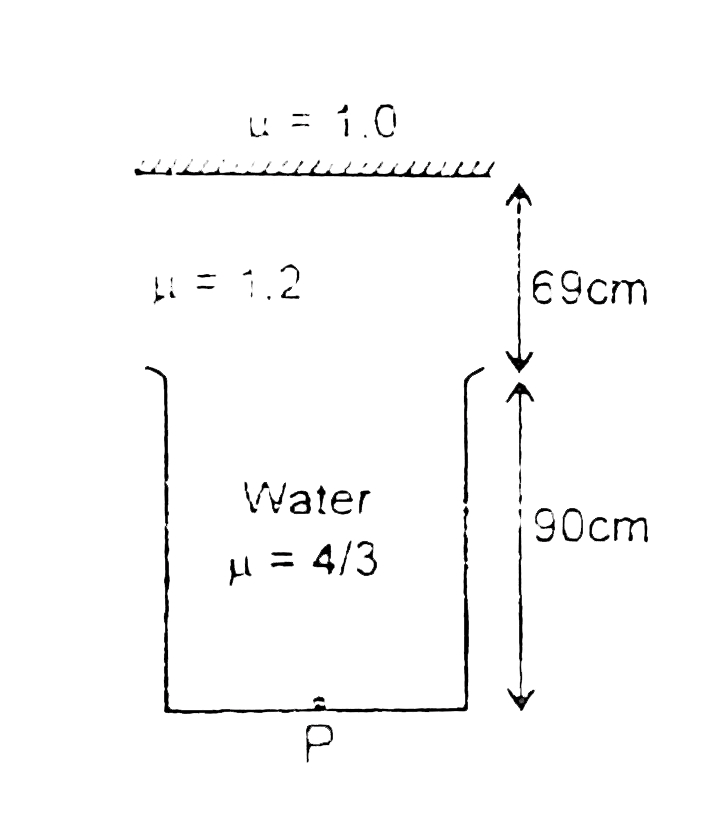 .
.
View SolutionWe have a vessel in shape of a cuboid partially filled with water. It base is square wilth an area of 4.5dm2(1dm=10cm) and a vessel contains water up to 2cm height. Then we place wooden cube inside water. The wood has mass 4kg and specific gavity 0.5. The base of the wooden cube is horizontal. Find the height of water level above the base of the wooden block.
View SolutionA solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm3of iron has approximately 8g mass.
View SolutionA cylindrical tank of height H is open at the top end and it has a radius r. Water is filled in it up to a height of h. The time taken to empty the tank through a hole of radius r' in its bottom is
View SolutionA long cylindrical tank of cross-sectional area 0.5m2 is filled with water. It has a small hole at a height 50cm from the bottom. A movable piston of cross-sectional area almost equal to 0.5m2 is fitted on the top of the tank such that it can slide in the tank freely. A load of 20kg is applied on the top of the water by piston, as shown in the figure. Calculate the speed of the water jet with which it hits the surface when piston is 1m above the bottom. (Ignore the mass of the piston)

View Solution
