A sphere and a right circular cylinder of the same radius have equal volume. By what percentage does the diameter of the cylinder exceed its height ?
To solve the problem step by step, we will follow the reasoning provided in the video transcript and derive the solution systematically.
Step 1: Understand the Problem
We have a sphere and a right circular cylinder with the same radius r and equal volumes. We need to find the percentage by which the diameter of the cylinder exceeds its height.
Step 2: Write Down the Volume Formulas
The volume V of a cylinder is given by:
Vcylinder=πr2h
The volume V of a sphere is given by:
Vsphere=43πr3
Step 3: Set the Volumes Equal
Since the volumes are equal, we can set the two equations equal to each other:
πr2h=43πr3
Step 4: Simplify the Equation
We can cancel π from both sides:
r2h=43r3
Now, divide both sides by r2 (assuming r≠0):
h=43r
Step 5: Find the Diameter of the Cylinder
The diameter d of the cylinder is given by:
d=2r
Step 6: Calculate the Percentage by Which the Diameter Exceeds the Height
We need to find the percentage by which the diameter exceeds the height:
Percentage=(d−hh)×100
Substituting the values of d and h:
Percentage=⎛⎝2r−43r43r⎞⎠×100
Step 7: Simplify the Expression
First, simplify the numerator:
2r−43r=63r−43r=23r
Now substitute this back into the percentage formula:
Percentage=⎛⎝23r43r⎞⎠×100
The r cancels out:
Percentage=(24)×100=12×100=50%
Final Answer
The diameter of the cylinder exceeds its height by 50%.
---
We have a sphere and a right circular cylinder with the same radius r and equal volumes. We need to find the percentage by which the diameter of the cylinder exceeds its height.
The volume V of a cylinder is given by:
Vcylinder=πr2h
The volume V of a sphere is given by:
Vsphere=43πr3
Since the volumes are equal, we can set the two equations equal to each other:
πr2h=43πr3
We can cancel π from both sides:
r2h=43r3
Now, divide both sides by r2 (assuming r≠0):
h=43r
The diameter d of the cylinder is given by:
d=2r
We need to find the percentage by which the diameter exceeds the height:
Percentage=(d−hh)×100
Substituting the values of d and h:
Percentage=⎛⎝2r−43r43r⎞⎠×100
First, simplify the numerator:
2r−43r=63r−43r=23r
Now substitute this back into the percentage formula:
Percentage=⎛⎝23r43r⎞⎠×100
The r cancels out:
Percentage=(24)×100=12×100=50%
The diameter of the cylinder exceeds its height by 50%.
Topper's Solved these Questions
Similar Questions
A right circular cylinder and a right circular cone have the same radius and the same volume. The ratio of the height of the cylinder to that of the cone is (a) 3:5 (b) 2:5 (c) 3:1 (d) 1:3
View SolutionThe curved surface area of a right circular cylinder of height 14 cmis 88 cm2. Find the diameter of the base of the cylinder.
View Solution
Knowledge Check
- Question 1 - Select One
If a right cylinder with a radius of 2 cm has a volume of 100πcm3, what is the height, in centimeters, of the cylinder?
A20B25C40D50 - Question 2 - Select One
The height and radius of the right circular cylinder below are given in meters. What is the volume, in cubic meters, of the cylinder?
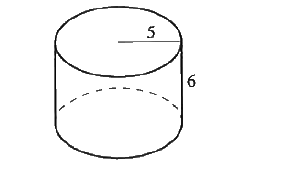 A30πB31πC150πD180π
A30πB31πC150πD180π - Question 3 - Select One
If a right circular cylinder of height 10 is inscribed in a sphere of radius 6, what is the volume of the cylinder ?
A104B346C545D785
The curved surface area of a right circular cylinder of height 14 cm is 88 cm2. Find the diameter of the base of the cylinder.
View SolutionA rocket is in the form of a right circular cylinder closed at the lower end and surmounted by a cone with the same radius as that of the cylinder. The diamter and height of the cylinder are 6 cm and 12 cm , respectively. If the slant height of the conical portion is 5 cm, the find the total surface area and volume of the rocket. ( use π=3.14).
View SolutionAn oil tank has the shape of a right circular cylinder is 12 centimeters in height and has a volume of 108π cubic centimeters. What is the diameter of the base of the cylinder, in centimeters?
View SolutionShow that the height of a closed right circular cylinder of given surface and maximum volume, is equal to the diameter of its base.
View SolutionShow that the height of a closed right circular cylinder of given surface and maximum volume, is equal to the diameter of its base.
View Solution

