A straight line through origin O meets the lines 3y=10−4x&8x+6y+5=0 at points A and B respectively. Then O divides the segment AB in the ratio:
3:4
1:2
2:3
4:1
The correct Answer is:D
Clearly, origin O is between the lines 4x+3y−10=0and8x+6y+5=0 . Equation of a line passing through the origin O is xcosθ=ysinθ. Let OP =r1andOQ=r2 . Then, the coordinates of P and Q are (r1cosθ,r1sinθ) and (r2cosθ,r2sinθ) respectively. These points lie on the lines 8x+6y+5=0and4x+3y−10=0 respectively.
∴r2(8cosθ+6sinθ)+5=0andr2(4cosθ+3sinθ)−10=0
⇒r1−−52(4cosθ+3sinθ)andr2=104cosθ+3sinθ

⇒r1=r24
⇒r2r1=−41
Hence , the required ratio is 4:1
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ILLUSTRATION 181videos
STRAIGHT LINES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Section I - Solved Mcqs64videos
STRAIGHT LINES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SETSEXERCISE - Chapter Test30videos
SETS
Similar Questions
A straight line through origin O meets the lines 3y=10−4x and 8x+6y+5=0 at point A and B respectively. Then , O divides the Segment AB in the ratio.
View SolutionA straight line through the origin 'O' meets the parallel lines 4x+2y=9 and 2x+y=−6 at points P and Q respectively. Then the point 'O' divides the segment PQ in the ratio
View SolutionA straight line through the point (2,2) intersects the lines √3x+y=0 and √3x−y=0 at the point A and B, respectively. Then find the equation of the line AB so that triangle OAB is equilateral.
View SolutionA straight line through the point (2,2) intersects the lines √3x+y=0 and √3x−y=0 at the point A and B, respectively. Then find the equation of the line AB so that triangle OAB is equilateral.
View SolutionA straight line through the point A (−2,−3) cuts the line x+3y=9 and x+y+1=0 at B and C respectively. If AB.AC=20 then equation of the possible line is
View SolutionThe line xa+yb=1 meets the axis of and y at A and B respectively and C is middle point of AB then
 View Solution
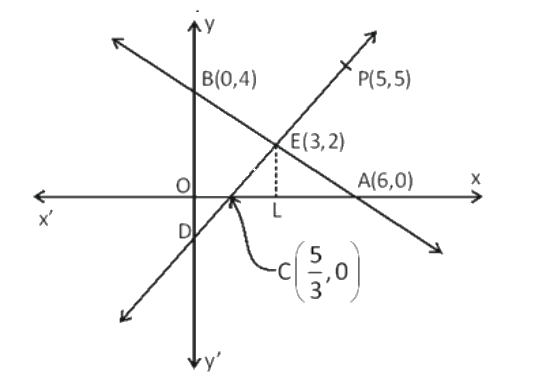
View SolutionThe line 2x+3y=12 meets the coordinates axes at A and B respectively. The line through (5, 5) perpendicular to AB meets the coordinate axes and the line AB at C, D and E respectively. If O is the origin, then the area (in sq. units) of the figure OCEB is equal to
 View Solution
View SolutionA straight line through A(−15−10) meets the lines x−y−1=0, x+2y=5 and x+3y=7 respectively at A, B and C. If 12AB+40AC=52AD prove that the line passes through the origin.
View SolutionThe line 2x+3y=12 meets the x-axis at A and y-axis at B. The line through (5,5) perpendicular to AB meets the x-axis and the line AB at C and E respectively. If O is the origin of coordinates, find the area of figure OCEB.
View SolutionA Line through the variable point A(1+k;2k) meets the lines 7x+y−16=0;5x−y−8=0andx-5y+8=0 at B;C;D respectively. Prove that AC;AB and AD are in HP.
View Solution
