[Bengali] A swimmer S is in the sea at a distance d km from the closes

A metal box with a square base and vertical sides is to contain $1024 c m^{3}$ of water, the material for the top and bottom costs Rs. $5 p e r c m^{2}$ and the material for the costs Rs. $2.50 p e r c m^{2}$ . Find the least cost of the box.

View Solution

A function is matched below against an interval where it is supposed to be increasing. Which of the following parts is incorrectly matched? Interval, Function [2, $\infty)$ , $2 x^{3} - 3 x^{2} - 12 x + 6$ $(- \infty, \infty)$ , $x^{3} = 3 x^{2} + 3 x + 3$ $(- \infty - 4)$ , $x^{3} + 6 x^{2} + 6$ $(- \infty, \frac{1}{3})$ , $3 x^{2} - 2 x + 1$

View Solution

Draw the graph of $f (x) = \frac{x^{2} - x + 1}{x^{2} + x + 1}$ .

View Solution

If $y = {cos}^{- 1} \sqrt{\frac{\sqrt{1 + x^{2} + 1}}{2 \sqrt{1 + x^{2}}}}, t h e n \frac{d y}{d x} i s e q u a < o$ $\frac{1}{2 (1 + x^{2})}, x \in R$ (b) $\frac{1}{2 (1 + x^{2})}, x > 0$ $\frac{- 1}{2 (1 + x^{2})}, x < 0$ (d) $\frac{1}{2 (1 + x^{2})}, x < 0$

View Solution

Let $f : R \to R, y = f (x), f (0) = 0, f' (x) > 0 and f'' (x) > 0$ . Three point $A (α, f (α)), B (β, f (β)), C (γ, f (γ)) o n y = f (x)$ such that $0 < α < β < γ .$
Which of the following is false ?

View Solution

A swimmer $S$ is in the sea at a distance $d k m$ from the closest point $A$ on a straight shore. The house of the swimmer is on the shore at distance $L k m$ from A. He can swin at speed oh ukm/h. walk at speed at vkm/h. At what point on shore should he land so that hhe reaches his house in the shortest time.

View Solution

A swimmer swims in still water at a speed =5 km//hr . He enters a 200m wide river, having river flow speed =4km//hr at point A and proceeds to swim at an angle of 127^(@) (sin 37^(@) = 0.6) with the river flow direction. Another point B is located directly across A on the other side. the swimmer lands on the other bank at a point C , form which he walks the distance CB with a speed = 3km//hr . The total time in which he reaches from A to B is

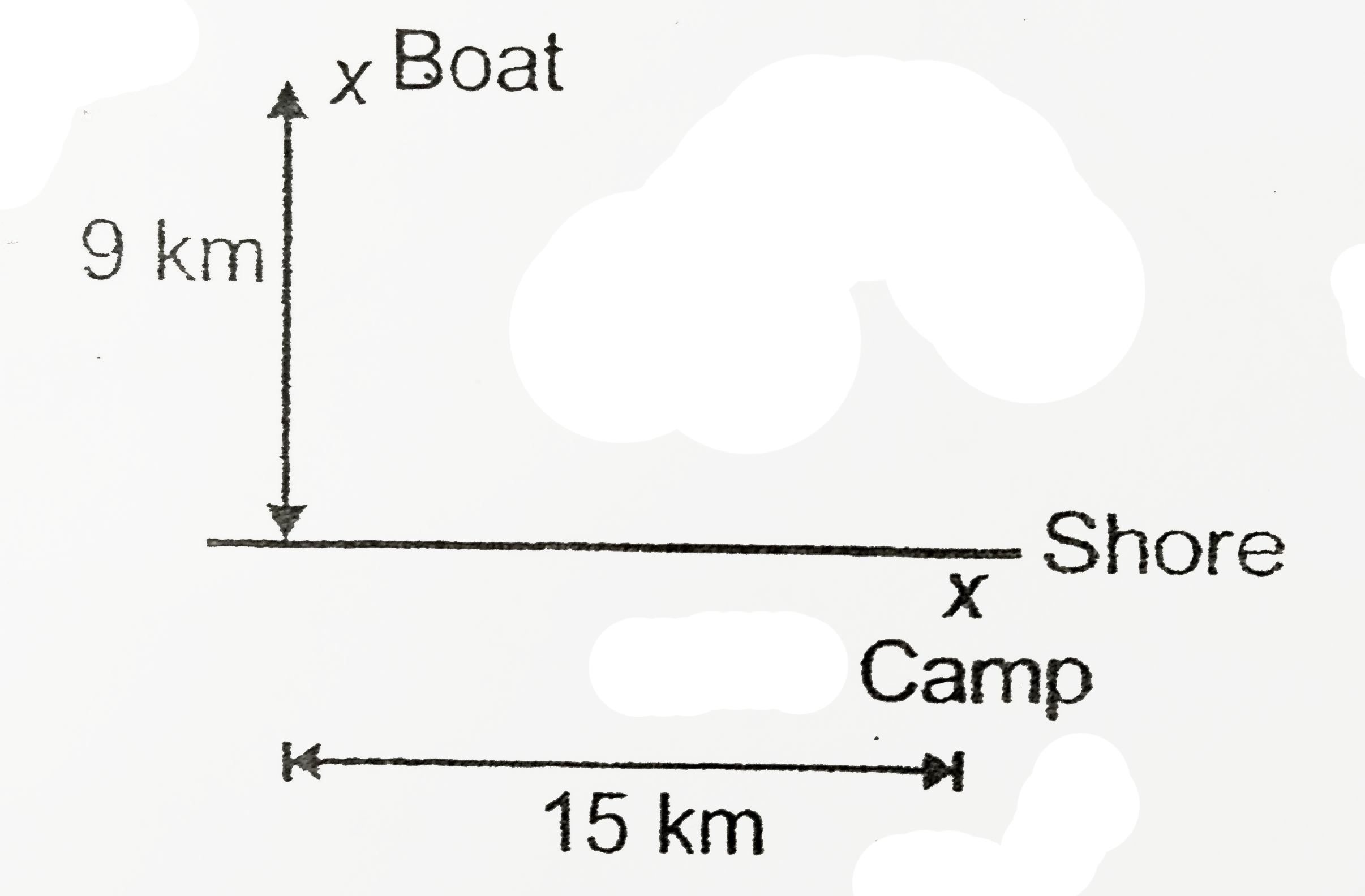
View Solution

A fishing boat is anchored 9 km away from the the nearest point on the shore. A messanger must be sent from the fishing boat to a camp, 15 km from the point on shore closest to boat. If the messanger can walk at a speed of 5 km per hour and can row at 4 km/h. determine the distance of that point (in km) from the shore, where he must land so as to reach the shore in least possible time.
ocr_image

View Solution

एक तैराक 5 km/h वेग से बह रही 500 m चौड़ी नदी को तैरकर पार करना चाहता है ।
तैराक को पैदल या तैरकर प्रारंभिक बिंदु के ठीक सामने दूसरे किनारे पर पहुँचना है । यदि वह तैरकर इस बिंदु से दूर कही निकलता है , तो उसे पैदल चलकर इस बिंदु तक आना पड़ेगा । उसे कम-से-कम कितनी दुरी पैदल चलना पड़ेगा ?

View Solution

एक तैराक S समुद्र में सीधे किनारे पर निकटतम बिन्दु A से d km दूरी पर है। तैराक का घर किनारे पर A से L km दूरी । पर है। वह ukm/hr की गति से तैर सकता है तथा $v k m / h r (v > u)$ की गति से चल सकता है। वह किनारे पर किस बिन्दु पर उतरे ताकि वह अपने घर पर सबसे कम संभव समय में पहुँच जाए ?

View Solution

A man can walk on the shore at a speed v_1 = 6 km/hr & swim in still water with a speed V_2 = 5 km/hr. If the speed of water is V_3 = 4 km/hr, at what angle should he head in the river in order to reach the exactly opposite point of the other shore in "shortest time including his swimming & walking?

View Solution

A swimmer $S$ is in the sea at a distance $d$ $k m$ from the closest point $A$ on a straight shore The house of the swimmer is at a distance $L$ km from $A$ on the shore. He can swim at a speed of $u k m$ / $h r$ and walk at a speed of $v k m$ / $h r (v > u)$ . At what point on the shore should he land so that he reaches his house in the shortest possible time?

View Solution

A swimmer swims in still water at a speed $= 5 k m / h r$ . He enters a 200 m wide river. Having river flow speed $= 4 k m / h r$ at point A and proceeds to swim at an angle of $127^{\circ}$ with the river flow direction. Another point B is located directly across A on the other side. The swimmer lands on the other bank at point C. from which he walks the distance CB with a speed $= 3 k m / h r$ . The total time (In minutes) in which he reaches from A to B is

View Solution

एक तैराक S समुद्र में सीधे किनारे पर निकटतम बिन्दु A से d km दूरी पर है। तैराक का घर किनारे पर A से L km दूरी । पर है। वह ukm/hr की गति से तैर सकता है तथा $v k m / h r (v > u)$ की गति से चल सकता है। वह किनारे पर किस बिन्दु पर उतरे ताकि वह अपने घर पर सबसे कम संभव समय में पहुँच जाए ?

View Solution

Mr. patel walked 6 km to reach the station from his house, then he boarded a train whose average speed was 60 km/hr and thus he reached his destination. In this way he took of 3 hours. If the average speed of the entire journey was 32 km/hr then the average speed of walking is :

View Solution

Does the escape speed of a body from the earth depend on.
(i)mass of the body
(ii)the location from where it is projected
(iii)the direction of projection
(iv)the height of the location from where the body is launched?

View Solution

The correct Answer is: $L - \frac{u d}{\sqrt{v^{2} - u^{2}}}$ km from his house

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS-Concept Application Exercise 6.6

The correct Answer is:L−ud√v2−u2 km from his house

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS-Concept Application Exercise 6.6

The correct Answer is: $L - \frac{u d}{\sqrt{v^{2} - u^{2}}}$ km from his house