
A system of inequalities and the corresponding graph are shown above. Which part of the graph could represent all of the solutions to the system?
A
A
B
B
C
C
D
D
Video Solution
Text Solution
The correct Answer is:D
Difficult:Medium:
Category: Heart of Algebra/ Inequalities
Strategic Advice: The solution to a system of inequalities is the region of the graph that satisfies both inequalities. Pay careful attention to which line is dashed and which solid as you analyze the regions of the graph.
Getting to the Answer: The solution set for the inequality y>x is the union of the sections of the graph that are above the dashed line, which are A and D. The solution set for the inequality 3y<−4x+6 is the union of the sections that are below set for the system of inequalities consists of all the points that satisfy both inequalities, which are contained within region (D).
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
y≤2x+2
y≥−3x−3
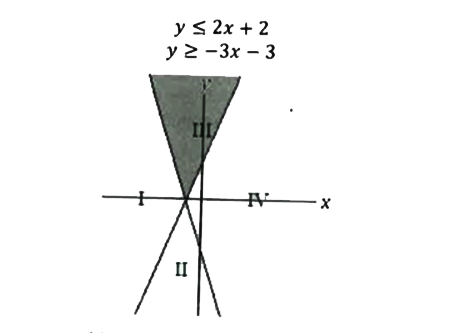
A system of inequalities and a graph are shown above. Which section or sections of the graph could represent all of the solutions to the system?ASection IBSection IVCSection II and IIIDSection I, II and IV{y>2x−35y≤3x

The graph above depicts the system of inequalities shown Which of the labeled section or sections of the graph could represent all of the solutions of the system ?ASection A and BBSection BCSection C and DDSection D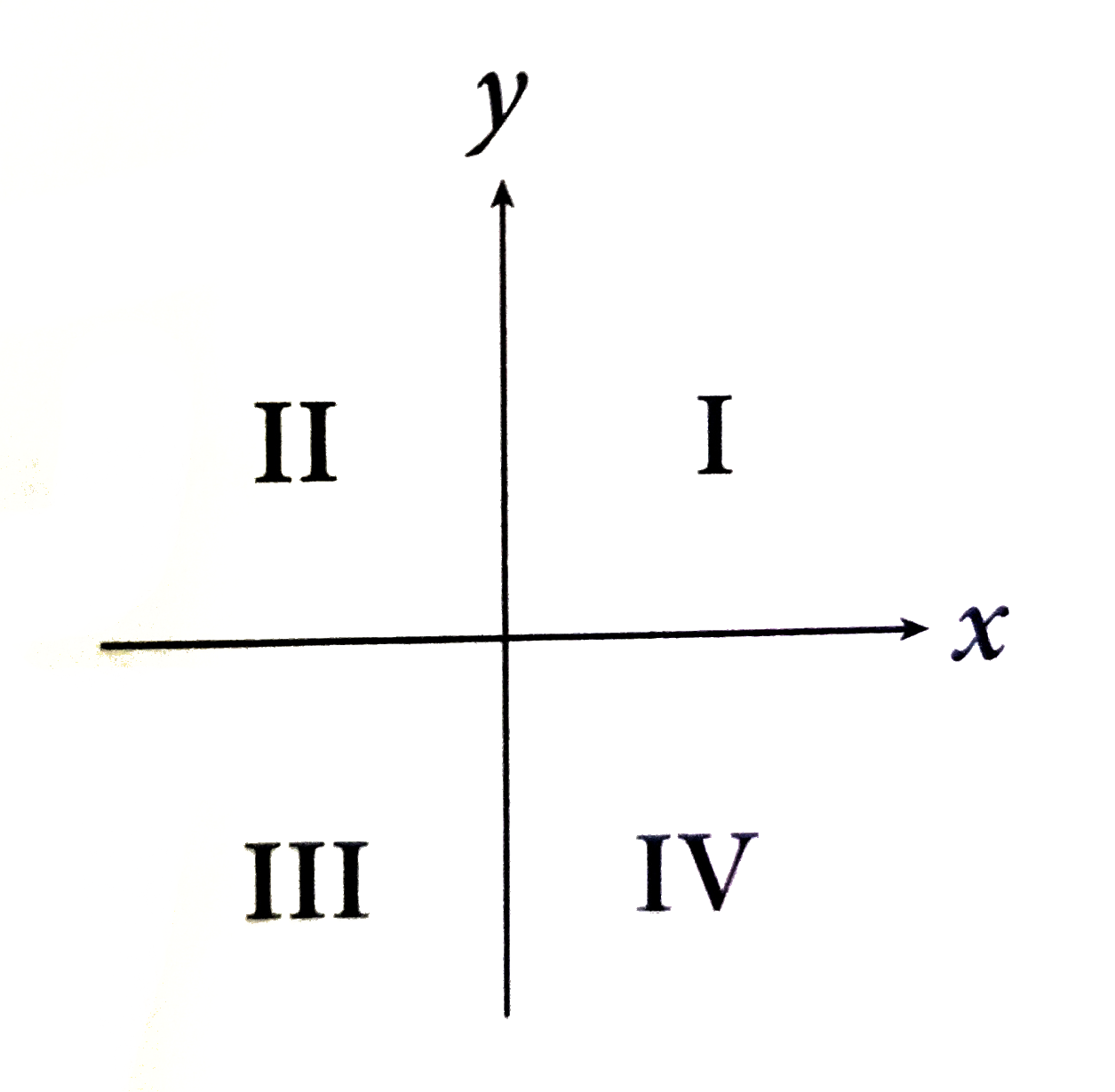
If the system of inequalities y≤−x+1andy<12x is graphed on the above polane which of the quadrants contain (s) no solutions to the system?AQuadrant IBQuadrant IICQuadrant IIIDQuadrants I and II
The inequality representing the following graph is
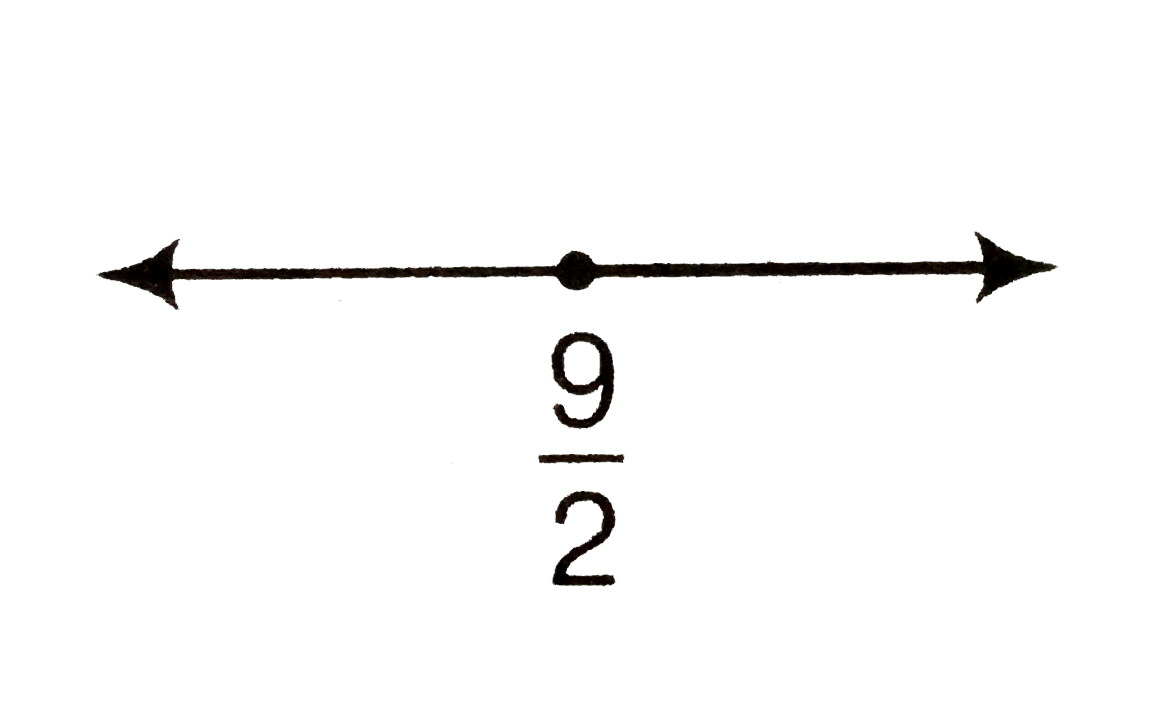
View SolutionThe inequality representing the following graph is

View Solution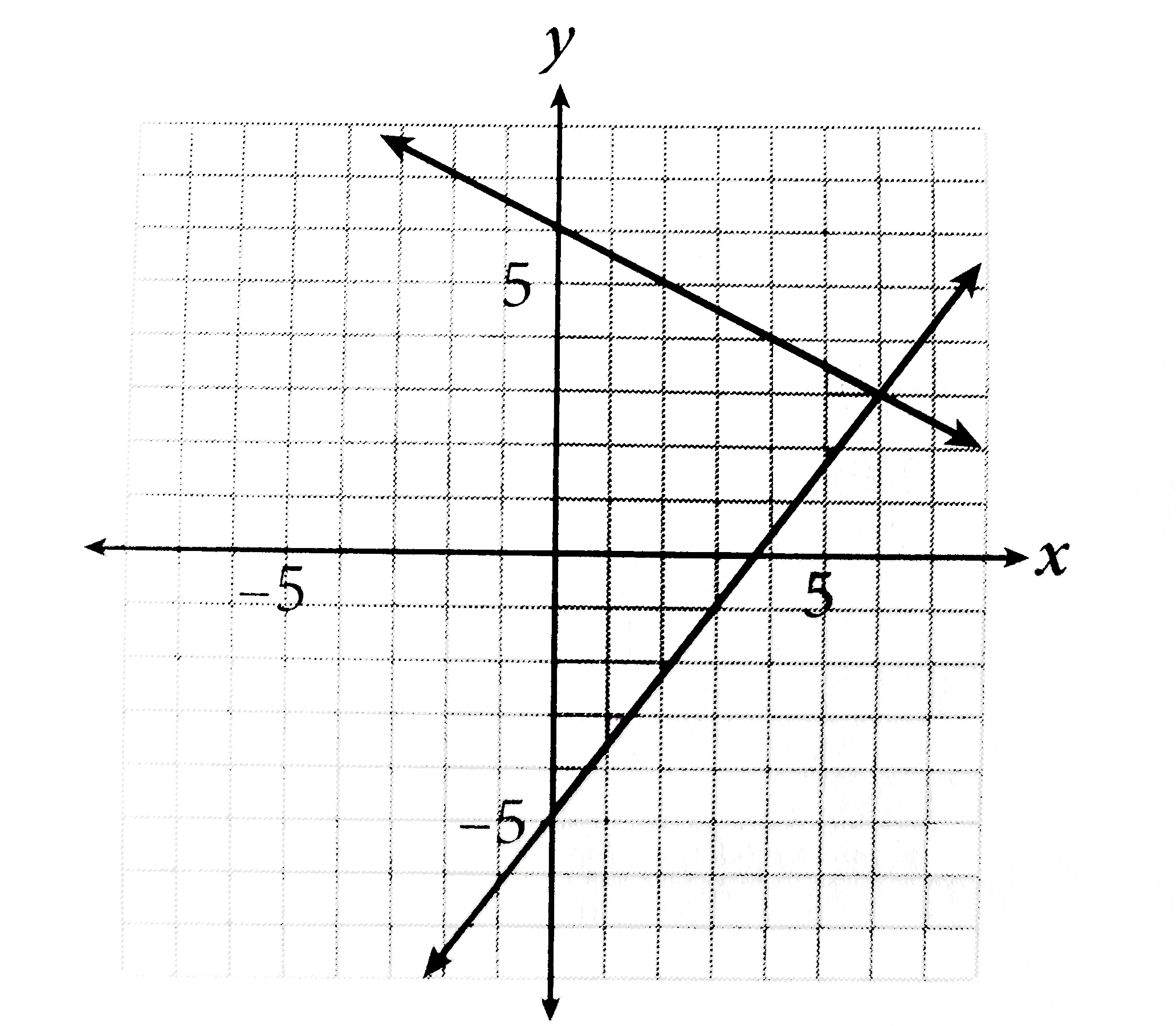
What is tha y-coordinate of the solution to the system shown above ?
View Solution
The graph shown represents which of the following equations ?
View Solution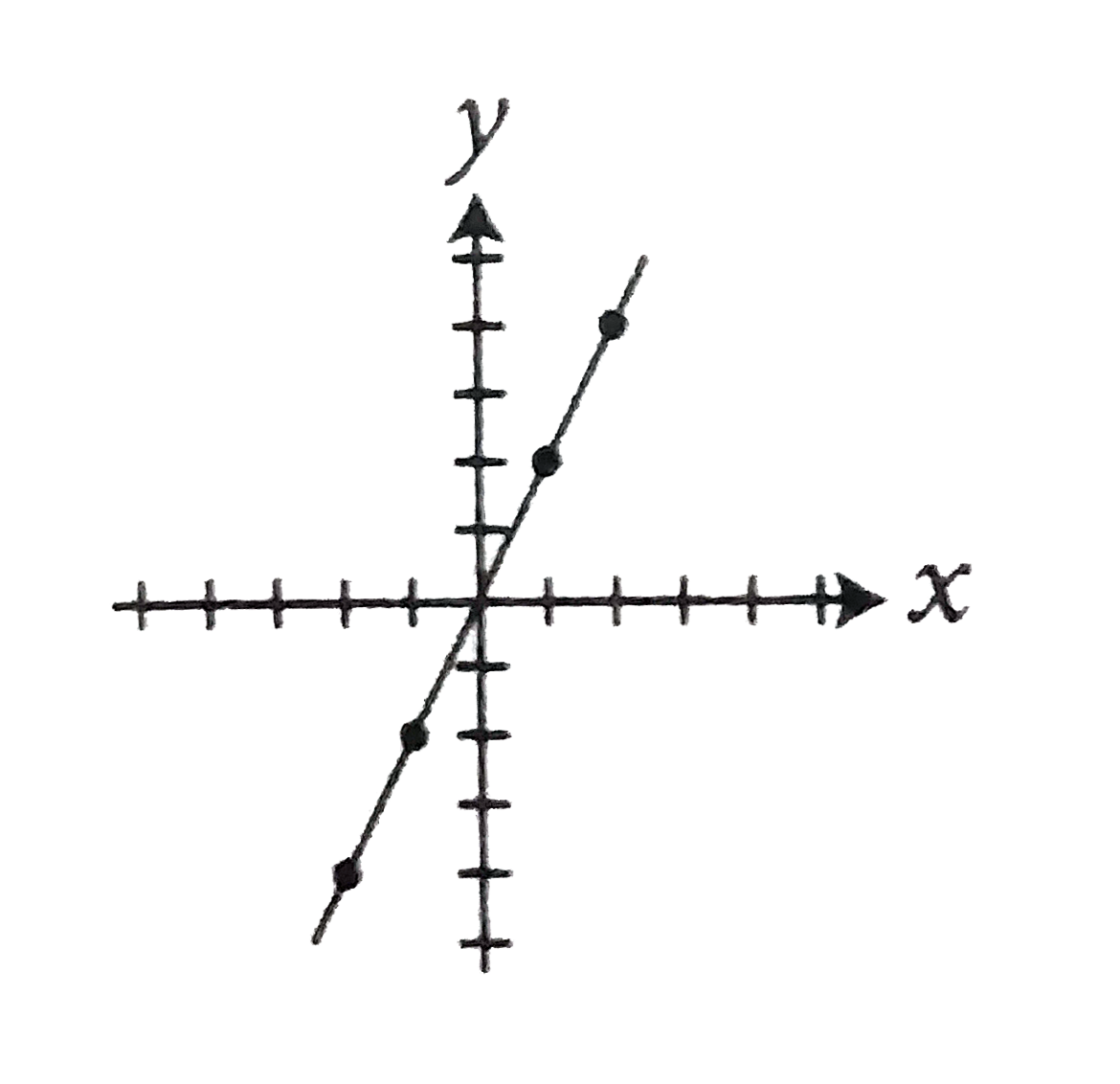
The graph above shows y=2x. Which of the following graphs represents y=|2x|?
View Solution


