A table screen has a 12-inch diagonal. If the length of the screen is √3 times longer than the width, what is the area, in square inches, of the screen ?
12
12√3
36
36√3
The correct Answer is:D
To solve the problem step by step, we will follow the information given in the question and use the Pythagorean theorem and the formula for the area of a rectangle.
Step 1: Define Variables
Let the width of the screen be W inches. According to the problem, the length L of the screen is √3 times the width:
L=√3⋅W
Step 2: Use the Pythagorean Theorem
Since the diagonal of the rectangle is given as 12 inches, we can apply the Pythagorean theorem. In a rectangle, the relationship between the length, width, and diagonal can be expressed as:
L2+W2=D2
where D is the diagonal. Substituting D=12:
L2+W2=122
L2+W2=144
Step 3: Substitute Length in Terms of Width
Now, substitute L with √3⋅W:
(√3⋅W)2+W2=144
Calculating (√3⋅W)2:
3W2+W2=144
Combine like terms:
4W2=144
Step 4: Solve for Width
Now, divide both sides by 4:
W2=1444=36
Taking the square root of both sides gives:
W=√36=6
Step 5: Find Length
Now that we have the width, we can find the length:
L=√3⋅W=√3⋅6=6√3
Step 6: Calculate the Area
The area A of the rectangle is given by:
A=L⋅W
Substituting the values of L and W:
A=(6√3)⋅6=36√3
Final Answer
Thus, the area of the screen is:
36√3 square inches
Let the width of the screen be W inches. According to the problem, the length L of the screen is √3 times the width:
L=√3⋅W
Since the diagonal of the rectangle is given as 12 inches, we can apply the Pythagorean theorem. In a rectangle, the relationship between the length, width, and diagonal can be expressed as:
L2+W2=D2
where D is the diagonal. Substituting D=12:
L2+W2=122
L2+W2=144
Now, substitute L with √3⋅W:
(√3⋅W)2+W2=144
Calculating (√3⋅W)2:
3W2+W2=144
Combine like terms:
4W2=144
Now, divide both sides by 4:
W2=1444=36
Taking the square root of both sides gives:
W=√36=6
Now that we have the width, we can find the length:
L=√3⋅W=√3⋅6=6√3
The area A of the rectangle is given by:
A=L⋅W
Substituting the values of L and W:
A=(6√3)⋅6=36√3
Thus, the area of the screen is:
36√3 square inches
Topper's Solved these Questions
- GEOMETRY BOOK - KAPLANCHAPTER - GEOMETRY EXERCISE - CIRCLES
1 Videos
- GEOMETRY BOOK - KAPLANCHAPTER - GEOMETRY EXERCISE - ARC LENGTH AND SECTORS
1 Videos
- GEOMETRY BOOK - KAPLANCHAPTER - GEOMETRY EXERCISE - THREE-DIMENSIONAL FIGURES
1 Videos
- FUNCTIONS BOOK - KAPLANCHAPTER - FUNCTIONS EXERCISE - DESCRIBING REAL-LIFE SITUATIONS WITH FUNCTIONS
1 Videos
- IMAGINARY NUMBERS BOOK - KAPLANCHAPTER - IMAGINARY NUMBERS EXERCISE - ARITHMETIC OPERATIONS WITH COMPLEX NUMBERS
1 Videos
Similar Questions
A landscape is designing a rectangular garden. The length of the garden is to be 5 feet longer than the width. IF the area of the garden will be 104 square feel, what will be the length in feet, of the garden?
View Solution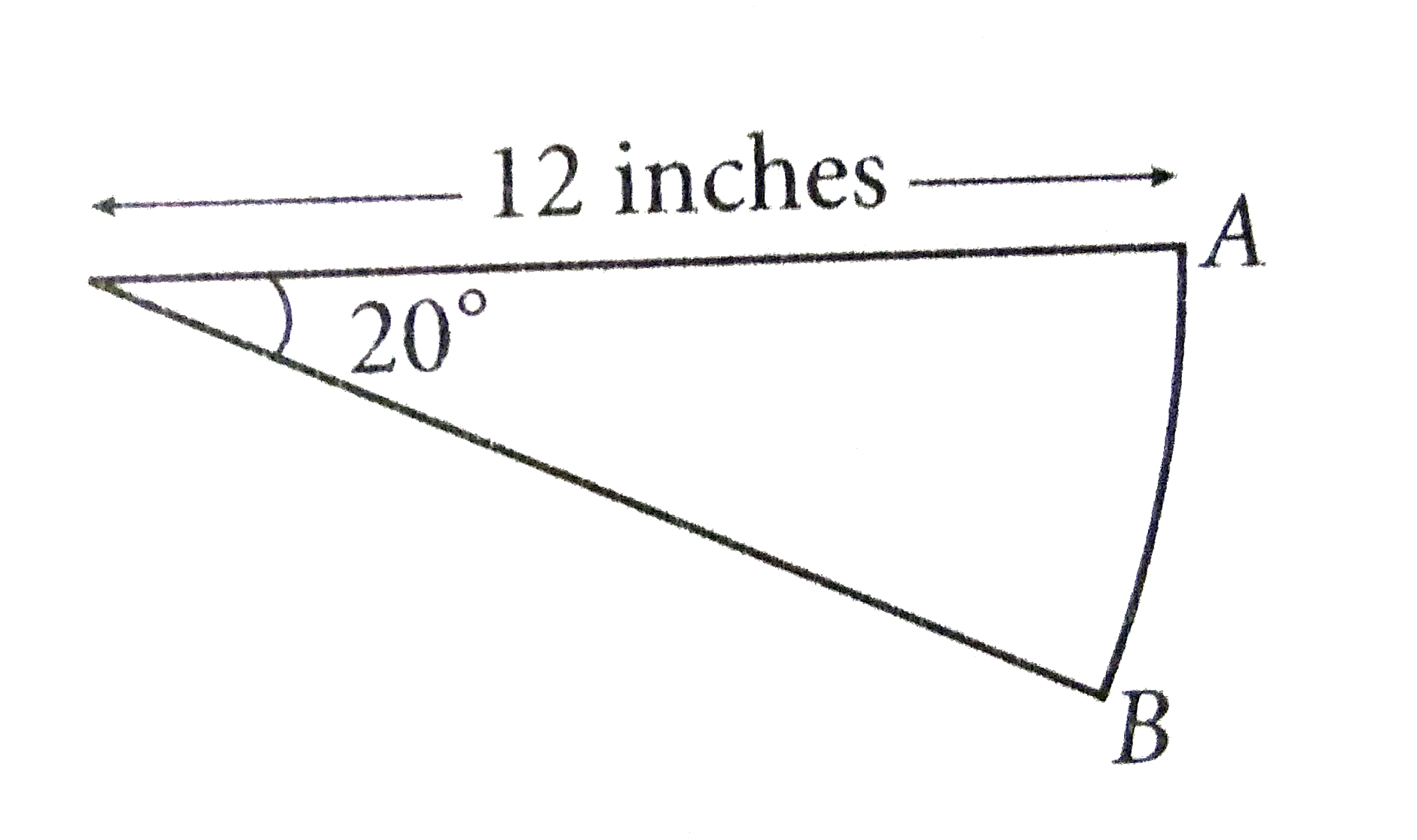
The figure above shows the path traced by the hand of a scale as it moves form A to B. What is the area, in square inches, of the region passed over by the scale's hand?
View Solution
Knowledge Check
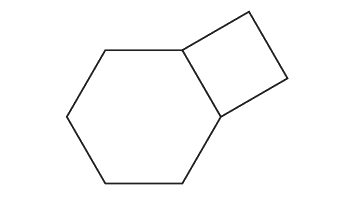
The figure above shows a regular hexagon with sides of length a and a square with sides of length a. If the area of the hexagon is 384 √3 square inches, what is the area, in square inches, of the square?A256B192C64√3D16√3A circle has a radius that is the same length as the sides of a square , if the square has a perimeter of 64 square inches , what is the area , in square inches , of the circle ?
A16B16πC32πD256πThe perimeter of square is 36 inches . What is the area of the square , in square inches ?
A6B9C18D81
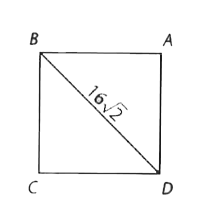
A square is bisected into two triangles (see figure). If the length of BD is 16√2 inches, what is the area of the square?
View SolutionGiven the figure below , what is the area of the trapezoid , in square inches ?

View SolutionWhat is the area of square with an diagonal of √2?
View SolutionA trapezoid has parallel bases that measure 3 inches and 9 inches and a height that measures 6 inches . What is the area, in square inches , of the trapezoid ?
View SolutionKen baked, frosted, and decorated a rectangular cake for the last Math Club meeting. The cake was 3 inches high, 12 inches wide, and 16 inches long. He centrated the cake on a piece of carboard whose rectangular top surface had been covered with aluminum foil, as shown in the figure below.
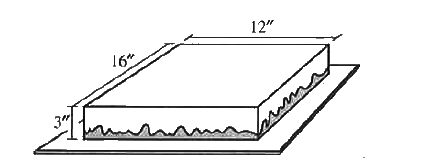
Ken used a piece of cardboard large enough to allow the cardboard to extend 2 inches beyond the cake on all sides. What is the area, in square inches, of the aluminum foil that is exposed on the top surface of the cardboard?
View Solution
