A tower subtends angles $α, 2 α, 3 α$ respectively, at point $A, B, a n d C$ all lying on a horizontal line through the foot of the tower. Prove that $\frac{A B}{B C} = 1 + 2 cos 2 α .$ Solution in Bengali

A

$\frac{3 sin α}{sin 2 α}$

B

$1 + 2 {cos}^{2} α$

C

$2 + {cos}^{3} α$

D

$\frac{sin 2 α}{sin α}$

Video Solution

Text Solution

Verified by Experts

Let PM the tower .

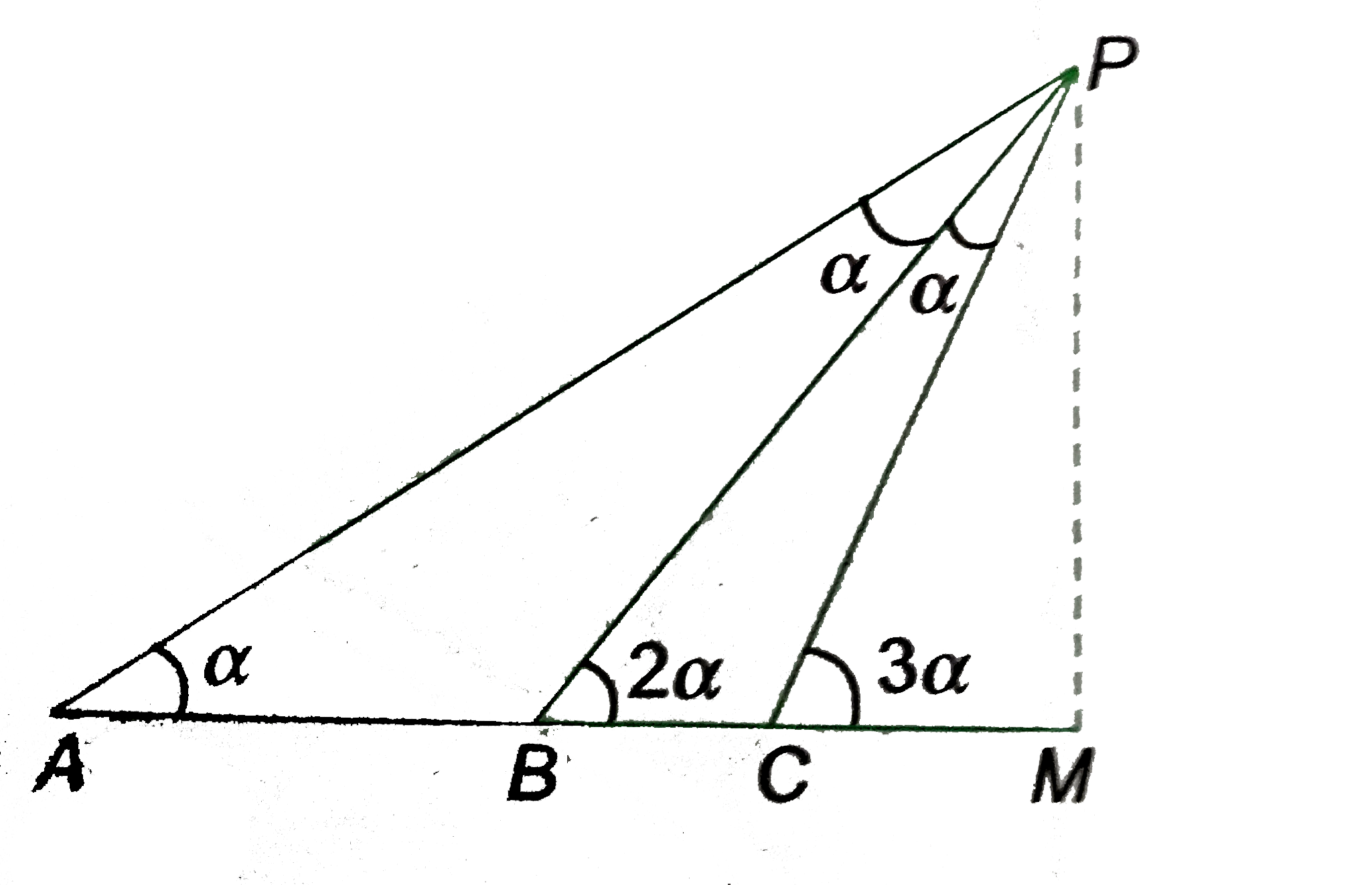
Given $∠ B A P = α, ∠ C B P = 2 α and ∠ M C P = 3 α$
$∴ ∠ A P B = ∠ P B C - ∠ B A P = 2 α - α = α$
Similarly, $∠ B P C = α$
$\Rightarrow B P = A B$
By sine formula in triangle BCP , we have
$\frac{B C}{sin (∠ B P C)} = \frac{B P}{sin (∠ B C P)}$
$\Rightarrow \frac{B C}{sin α} = \frac{A B}{sin (180^{\circ} - 3 α)}$
$\Rightarrow \frac{A B}{B C} = \frac{sin 3 α}{sin α} = \frac{3 sin α - 4 {sin}^{3} α}{sin α}$
$= 3 - 4 {sin}^{2} α$
$= 3 - 2 (1 - cos 2 α)$
$= 1 + 2 cos 2 α$

|

Class 12 MATHS HIGHT AND DISTANCE

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-HIGHT AND DISTANCE -Exercises

Home
Ask Doubt
Profile