A triangle ABC is inscribed in a circle with centre at O, The lines AO,BOandCO meet the opposite sides at D,E,andF, respectively. Prove that 1AD+1BE+1CF=acosA+bcosB+osC△Solution in Punjabi
The correct Answer is:2
Step by step video & image solution for A triangle A B C is inscribed in a circle with centre at O , The lines A O ,B Oa n dC O meet the opposite sides at D , E ,a n dF , respectively. Prove that 1/(A D)+1/(B E)+1/(C F)=(acosA+bcosB+ccosC)/triangle by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - PROPERTIES AND SOLUTIONS OF TRIANGLES EXERCISE 6 : SINGLE INTEGER ANSWER TYPE QUESTIONS
1 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Subjective Type Questions)
21 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - PROPERTIES AND SOLUTIONS OF TRIANGLES EXERCISE 5: MATCHING TYPE QUESTIONS
4 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
52 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Find the value of trigonometric function cos(2π3)
View SolutionIn a ΔABC, the angles A and B are two values of θ satisfying √3cosθ+sinθ=k, where |K|<2, then show triangles is obtuse angled.
View SolutionMatch the statement of Colume I with values of Column II.
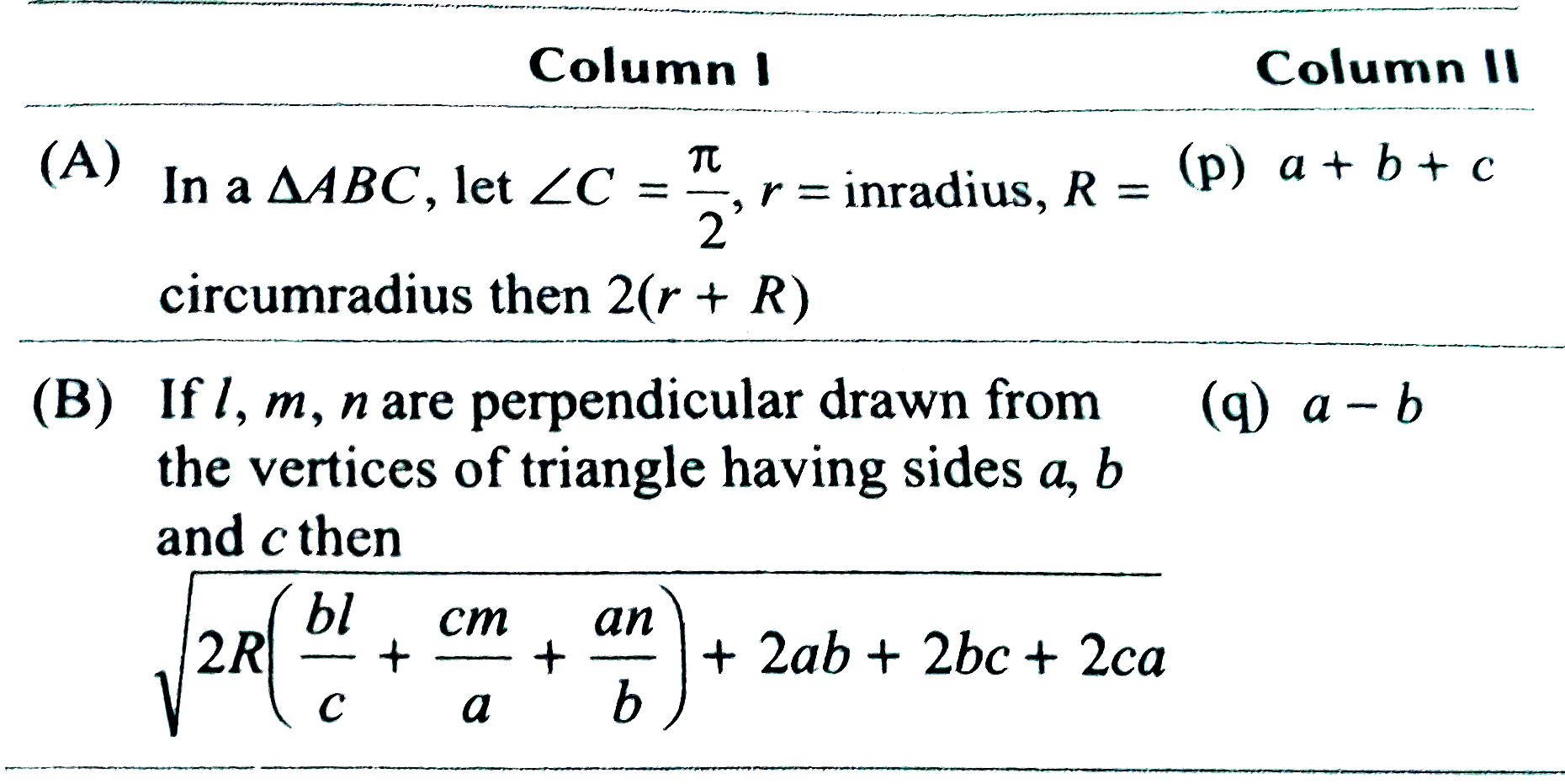
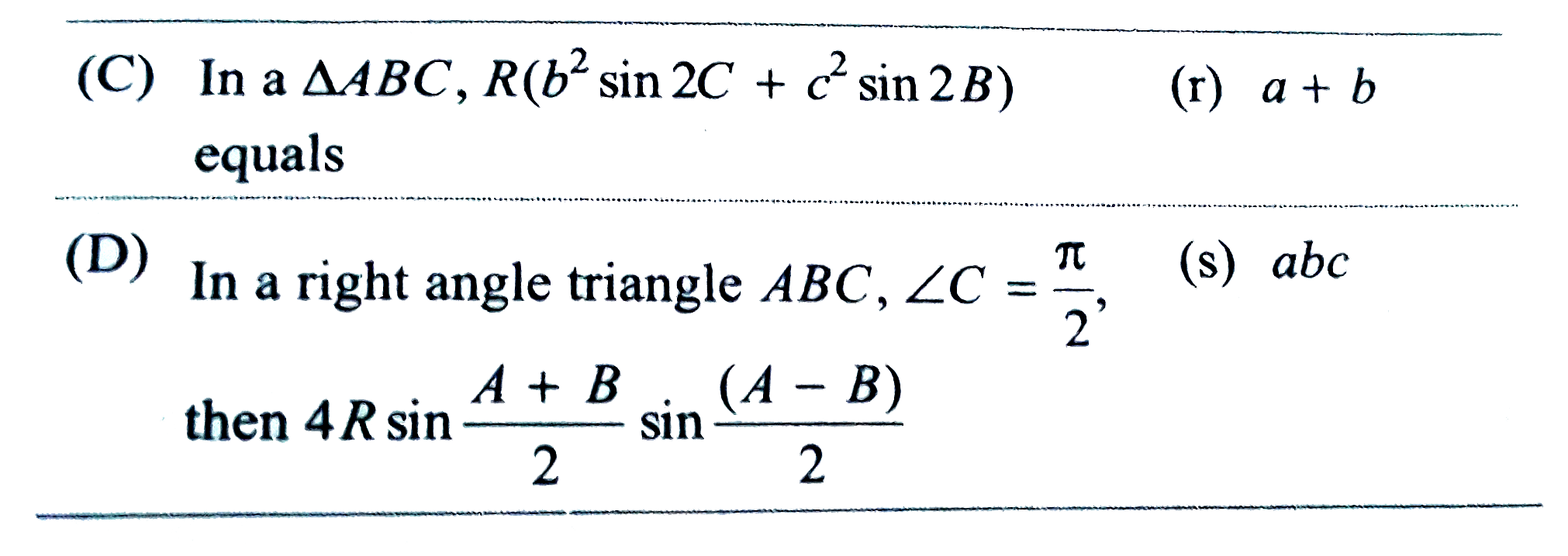
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as its
View SolutionLet a,b,c be in A.P. and |a|<1,|b|<1|c|<1.ifx=1+a+a2+....to ∞,y=1+b+b2+....to ∞and,z=1+c+c2+...to ∞, then x,y,z are in
View SolutionIf O is a point in space, ABC is a triangle and D,E,F are the mid-points of the sides BC,CA and AB respectively of the triangle, prove that →OA + →OB+→OC=→OD+→OE+→OF.
View SolutionA triangle ABC is inscribed in a circle with centre at O, The lines AO,BOandCO meet the opposite sides at D,E,andF, respectively. Prove that 1AD+1BE+1CF=acosA+bcosB+osC
View SolutionFill the blanks in the following so that each of the following statements is true.
(i) Sides opposite to equal angles of a triangle are ......
(ii) Angle opposite to equal sides of a triangle are .....
(iii) In an equilateral triangle all angles are .....
(iv) In a ΔABC if ∠A = ∠C , then AB = ......
(v) If altitudes CE and BF of a triangle ABC are equal, then AB = ....
(vi) In an isosceles triangle ABC with AB = AC, if BD and CE are its altitudes, then BD is …… CE.
(vii) In right triangles ABC and DEF, if hypotenuse AB = EF and side AC = DE, then ΔABC ≅ Δ ……
View SolutionD,E,andF are the middle points of the sides of the triangle ABC , then (a) centroid of the triangle DEF is the same as that of ABC (b) orthocenter of the tirangleDEF is the circumcentre of ABC
View SolutionIn triangle ABC ,points D,EandF are taken on the sides BC,CAandAB, respectively, such that BDDC=CEEA=AFFB=n. Prove that △DEF=n2−n+1(n+1)2△(ABC).
View SolutionFrom a point O inside a triangle ABC, perpendiculars OD,OEandOf are drawn to rthe sides BC,CAandAB, respecrtively. Prove that the perpendiculars from A,B,andC to the sides EF,FDandDE are concurrent.
View SolutionIf O is a point in space, ABC is a triangle and D,E,F are the mid-points of the sides BC,CA and AB respectively of the triangle, prove that →OA + →OB+→OC=→OD+→OE+→OF.
View SolutionIn a △ ABC, If L and M are points on AB and AC respectively such that LM∣∣BC. Prove that: ar (△ LOB)=ar (△ MOC)
View SolutionD is the mid-point of side BC of △ABC and E is the mid-point of BD. If O is the mid-point of AE , prove that ar(△BOE)=18ar(△ABC).
View SolutionIn Figure, OA and OB ar respectively perpendiculars to chords CD and EF of a circle whose centre is O. If OA=OB , prove that CE=DF.
View SolutionO is any point inside a triangle ABC . The bisector of ∠AOB,∠BOC and ∠COA meet the sides AB,BC and CA in point D,EandF respectively. Show that AD⋅BE⋅CF=DB⋅EC⋅FA
View Solution
