Question

A triangle $ABC$ is drawn to circumscribe a circle of radius $4cm$ such that the segments $BD$ and $DC$ into which $BC$ is divided by the point of contact $D$ are of lengths $6cm$ and $8cm$ respectively. Find the lengths of the sides $AB$ and $AC$.

Explanation

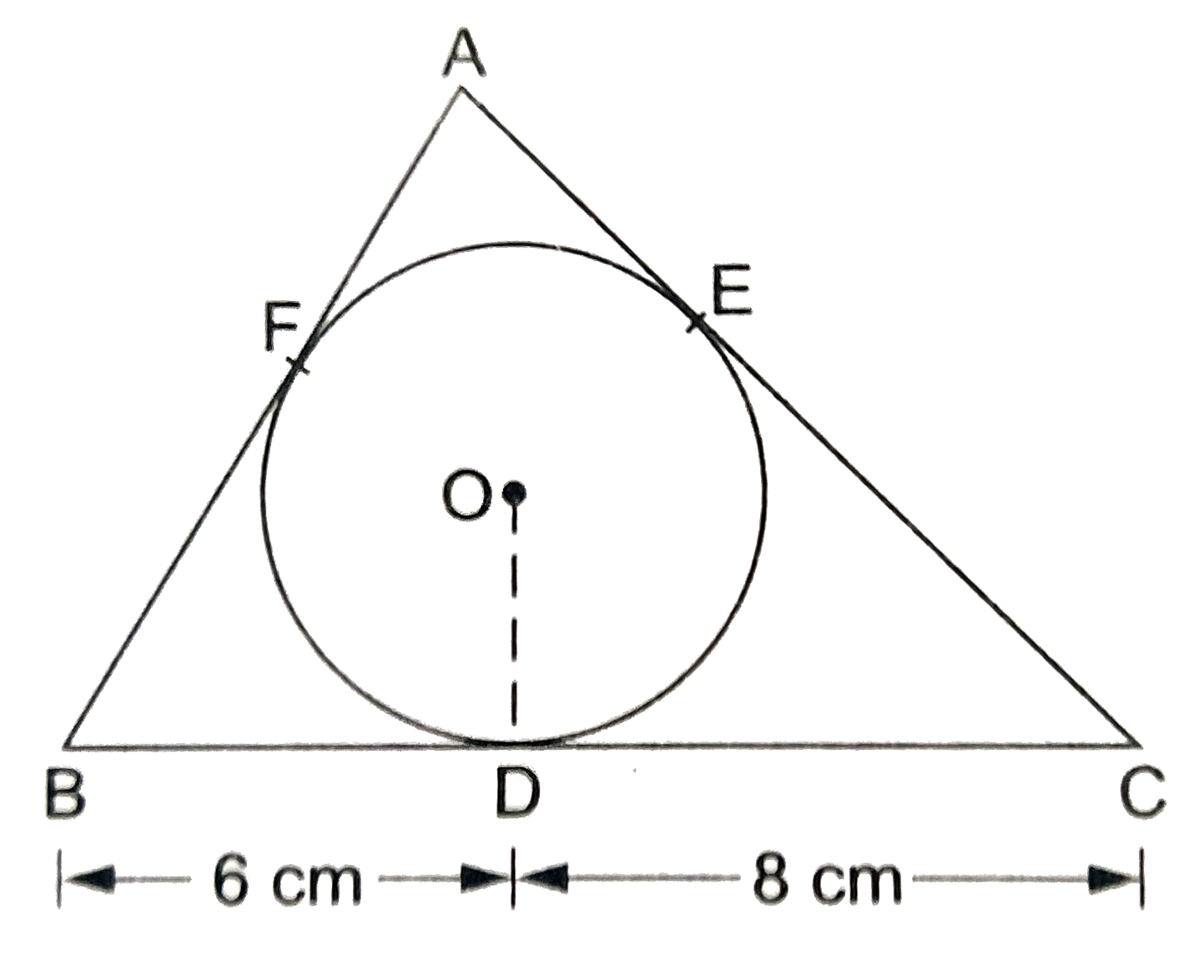
Length of two tangents drawn from the same point to the circle are equal.

`CF = CD = 6 cm`

` BE = BD = 8 cm`

` AE = AF = x`

We observed that,

`AB = AE + EB = x + 8`

`BC = BD + DC = 8 + 6 = 14`

`CA = CF + FA = 6 + x`

Let perimeter of triangle ABC be s.
` 2s = AB + BC + CA`

`= x + 8 + 14 + 6 + x`

`= 28 + 2x`

` s = 14 + x`

Area of triangle ABC =

`=sqrt(s(s-a)(s-b)(s-c))`

`=sqrt((14+x)48x)` ...(i)

Also, area of triangle ABC = 2
× (area of triangle AOF + COD + DOB)

`=2xx[1/2xxOFxxAF + 1/2xxCDxxOD + 1/2xxDBxxOD]`

`=56+4x` ...(ii)


Equating equations (i) and (ii) we get,

`x=7`

Hence, `AB = x + 8 = 7 + 8 = 15 cm`

`CA = 6 + x = 6 + 7 = 13 cm.`